Quando falamos em Sistema Price, não devemos deixar de mencionar a Tabela Price. E quando citamos essa tabela, devemos falar da fórmula que permite o cálculo dos coeficientes da mesma. A fórmula da Tabela Price nada mais é do que uma equação que determina, para uma determinada taxa de juros e uma fixada quantidade total de pagamentos periódicos, um coeficiente que tem por objetivo facilitar a obtenção do valor das iguais parcelas de um financiamento ou empréstimo sob regime de juros capitalizados. Esse sistema em estudo neste artigo tem como núcleo a fórmula da Tabela Price. Matematicamente, o Sistema Price é identificado pela sigla "SFA", que significa Sistema Francês de Amortização. Richard Price foi um matemático que viveu no século XVIII e trabalhou, com dedicação, utilizando os princípios atrelados a esse assunto.
Nessa dinâmica, a Tabela Price não é o quadro de amortização (demonstrativo) que indica a posição mês a mês do saldo devedor, como muitos mutuários pensam. Além disso, entre outros esclarecimentos, deve-se também dizer que existe uma tabela para cada taxa de juros ao período de pagamentos que informa os coeficientes para várias quantidades de parcelas do prazo total do financiamento. Por exemplo, para 5% temos o coeficiente 0,06043446 na linha 36 da tabela, indicando que se multiplicarmos esse coeficiente pelo valor financiado, teremos como resultado o valor das iguais 36 prestações que devem ser pagas periodicamente a fim de, sob regime de juros compostos, quitar o financiamento. Em um exemplo onde financiamos R$ 15.000,00, devemos pagar 36 prestações de R$ 906,52 em relação à taxa de juros informada. A taxa original da tabela sempre está vinculada ao período de pagamentos. Observe que se financiarmos R$ 15.000,00, poderemos pagar 36 prestações mensais de R$ 906,52 por meio da taxa de juros de 5% ao mês. Note também que se financiarmos R$ 15.000,00, poderemos pagar 36 prestações anuais de R$ 906,52 por meio da taxa de juros de 5% ao ano. Vale relembrar que a taxa original da tabela é aquela que está associada ao período de pagamentos.
Na equação acima é possível notar a expressão: "(1+0,05) elevada à potência 36". Isso é o mesmo que multiplicarmos várias vezes a expressão "(1+0,05)" por ela mesma. Essa expressão aparece no numerador e também no denominador da equação e representa o Fator acumulado de capitalização, resultante do prazo de 36 períodos. Efetuando o cálculo desse fator citado, encontramos como resultado 5,791816136. A partir desse momento, a obtenção do resultado do valor das iguais prestações pela Tabela Price já está bem mais próxima, visto que, como já dito, o fator mencionado aparece no numerador e no denominador da equação, bastando, então, realizar a substituição na mesma. Observe abaixo como ficou mais confortável o trabalho de resolução da equação:
Observe abaixo o demonstrativo de evolução do saldo devedor tradicional, também chamado de quadro de amortização. Nele, a capitalização de juros não é aparente, em virtude do modo (padrão) como ele é construído. Inicialmente, a fim de facilitar a monitoração do comportamento das quatro variáveis ao longo do prazo, consideremos, em nosso exemplo, que todos os pagamentos possuam a periodicidade mensal.
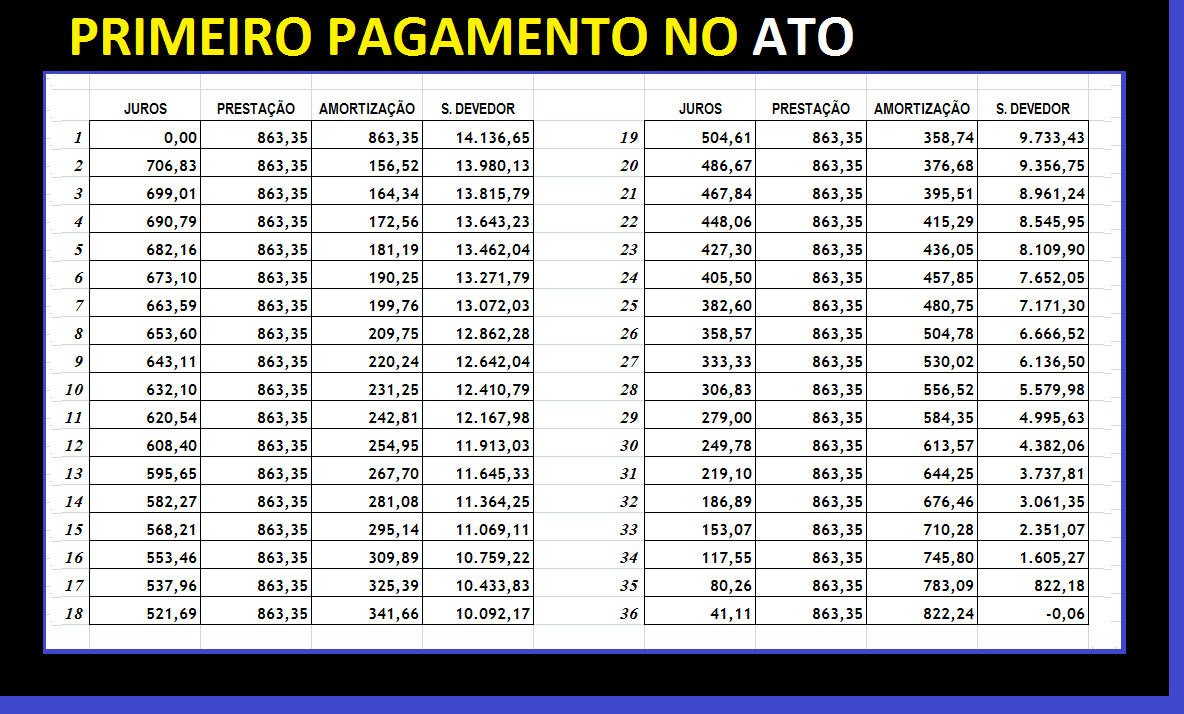
Continuando nosso raciocínio e aproveitando esse exemplo, podemos dizer que se o contrato estabelecesse que o momento do primeiro pagamento coincidisse com a data de assinatura do mesmo, teríamos, por esse motivo, a obrigação de que a primeira parcela fosse paga no ato da contratação. Nesse caso não precisaríamos de outra fórmula específica para determinarmos o valor das iguais prestações mensais que satisfizesse essa comum condição. Assim, bastaríamos, portanto, dividir o valor acima por "(1+taxa/100)", sendo R$ 906,52 dividido por 1,05. O valor das iguais prestações seria de R$ 863,35. O valor financiado nesse caso seria de R$ 14.136,65. Isso ocorreria porque o valor contratado de R$ 15.000,00 seria diminuído pela entrada de R$ 863,35 referente à primeira prestação. Nessa trilha, note que os valores estão corretos na medida em que se procurássemos, por exemplo, o coeficiente na Tabela Price atrelada a 5% ao mês, com somente 35 meses, teríamos o coeficiente de 0,06107171. O valor real financiado aplicado de R$ 14.136,65 multiplicado por 0,06107171 resultaria no valor das iguais prestações de R$ 863,35.
Observe abaixo o demonstrativo de evolução do saldo devedor tradicional. Por meio dele, note que o saldo devedor, como explicado acima, se torna R$ 14.136,65 após o primeiro pagamento, restando, por essa razão, as realizações dos pagamentos de número 2 ao 36. O valor inicial contratual foi de R$ 15.000,00, entretanto, como é possível notar detalhadamente no demonstrativo, o valor financiado, de fato, foi de R$ 14.136,65. Do pagamento de número 2 ao 36 existem 35 pagamentos (quantidade de parcelas introduzida na equação acima). Ressaltando que, nesse exemplo de financiamento com pagamentos antecipados em um período, obviamente e sem dúvida alguma, com exceção da entrada (primeira prestação sem juros) e também da segunda prestação (com vencimento após somente um período de capitalização), todas as demais parcelas até a última possuiriam juros sobre juros em seu interior.
Existe também a comum possibilidade de que o financiamento ou empréstimo possua a carência de um período (30 dias) para início dos pagamentos, ou seja, a primeira parcela acaba sendo devida, desse modo, depois de dois períodos (60 dias) da assinatura do contrato. Nesse caso não precisaríamos também de outra fórmula específica para determinarmos o valor das iguais prestações mensais que satisfizesse essa outra comum condição. Dessa forma, bastaríamos, portanto, ao invés de dividir, multiplicar o valor calculado padrão (referente à modalidade em pagamentos postecipados) por "(1+taxa/100)", sendo R$ 906,52 multiplicado por 1,05. O valor das iguais prestações seria de R$ 951,84.
Observe abaixo o demonstrativo de evolução do saldo devedor tradicional. Nesse terceiro plano em especial, onde o primeiro pagamento ocorre após 60 dias da assinatura do contrato, os juros calculados na primeira linha do demonstrativo são de R$ 1.537,50. Como já calculado, o valor da prestação é de R$ 951,84 e, por causa disso, o saldo devedor aumentou após realizado o pagamento, em R$ 585,66, passando de R$ 15.000,00 para R$ 15.585,66. Por consequência da utilização dessa ótica tradicional, acredita-se erradamente que somente nessa etapa, quando isso acontece, contou-se, assim, juros sobre juros no cálculo desse encargo para o mês seguinte. Nessa trilha, equivocadamente se diz que não são contados juros sobre juros em todas as outras etapas, referentes aos demais meses, na medida em que os saldos devedores foram sempre menores em comparação com os dos meses imediatamente anteriores. Isso é uma ilusão de milhares de brasileiros, já que, na realidade, em todas as etapas, ou seja, em todos os meses houve contagem de juros sobre juros. Não importa se o saldo devedor é maior ou menor em relação ao calculado no mês anterior, pois, comprovadamente, posso garantir que sempre que os juros forem calculados sobre o saldo devedor, existirá contagem de juros sobre juros. A razão de parecer o contrário está no modo como está estruturado o demonstrativo de evolução do saldo devedor tradicional. A estrutura do demonstrativo citado não possui a intenção de esconder a capitalização de juros, visto que o objetivo principal é proporcionar grande praticidade em sua construção, sem a necessidade de uso de calculadoras. A variável saldo devedor exibe corretamente a precisa realidade em todos os meses, sendo esse o motivo da utilização desse tipo de quadro no mercado de crédito. Apesar disso, é importante que o mutuário saiba que o Sistema Francês de Amortização, relativo ao uso da Tabela Price, aplica juros sobre juros em todos os períodos mensais, mesmo que isso não esteja evidente, mediante a utilização do quadro tradicional.
Este artigo foi escrito com extrema clareza e com nítidas ilustrações propositalmente por duas importantes razões. A primeira por causa de informações equivocadas que estão presentes na Internet e demais ambientes do mundo digital, gerando muitas dúvidas ou distanciando, sem intenção, mutuários e profissionais do caminho que leva à literatura de natureza acadêmica, a fim de tirarem conclusões corretas com referência ao tema. O segundo motivo da construção deste trabalho de forma clara, foi de mostrar que o assunto é possível de ser compreendido por todos, ao contrário do que muitos mutuários acreditam, por trabalharem em áreas que não utilizam no cotidiano, de modo algébrico, os conceitos da ciência matemática. Por fim, gostaria de dar um conselho a respeito do que percebi em minha época de faculdade: "Algo aparentemente difícil de entender é, na verdade, um conjunto de vários e interligados detalhes muito fáceis de serem compreendidos. A dificuldade não está presente em nenhum assunto, todavia, então, na ilusão de que ele não é fácil". Nesse pensamento, leia o importante artigo que escrevi a respeito da comprovação da também existência de capitalização de juros no outro sistema de amortização muito utilizado no Brasil, conhecido como Sistema de Amortização Constante (SAC). O artigo citado foi selecionado pelos editores do portal Jus.com.br e publicado na Revista Jus Navigandi (revista eletrônica), juntamente com o fornecimento de um documento de declaração de publicação, datado em 12 de julho de 2020. A revista é registrada no IBICT (Instituto Brasileiro de Informação em Ciência e Tecnologia), órgão vinculado ao Ministério da Ciência e Tecnologia, responsável pela catalogação internacional de publicações periódicas, sob o código ISSN 1518-4862. Todos os textos que são publicados na revista são submetidos a apreciação prévia. Seu conselho editorial foi formalmente constituído em abril de 2009. Em razão disso, por meio do link exposto a seguir, não deixe de ter acesso ao selecionado artigo: https://jus.com.br/artigos/79654/sistema-de-amortizacao-constante-sac-aplica-juros-sobre-juros