Inicialmente é importante explicar como são calculadas as variáveis que compõem o sistema SAC. Este é um sistema de amortização de financiamentos e empréstimos que foi criado a partir de uma convenção de natureza operacional. Por essa razão, quando utilizado, torna-se impossível ao mutuário notar a aplicação de juros sobre juros, visto que o quadro de amortização tradicional, conhecido também como demonstrativo de evolução do saldo devedor, está em sintonia com o próprio método de cálculo desse sistema em estudo neste artigo.
A princípio é calculada a parcela constante de amortização, também chamada como "cota de amortização". Ela é fruto da divisão do valor financiado pela quantidade de pagamentos periódicos (sendo a periodicidade mensal encontrada com frequência nos contratos) e, por sua vez, os juros, a cada mês, são calculados sobre o saldo devedor do mês anterior e somados à cota de amortização já inicialmente calculada, formando, então, o valor da prestação a ser pago do mês. Nesse caminho e por esse motivo, as prestações acabam sendo decrescentes ao longo do prazo total do financiamento ou empréstimo, porque os juros diminuem gradativamente, consequentes do saldo devedor que vai sendo reduzido com os pagamentos mensais ocorridos.
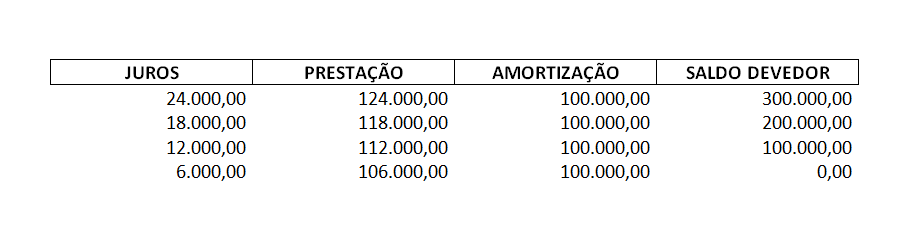
Observe o exemplo de financiarmos R$ 400.000,00 em 4 prestações mensais, mediante a taxa de juros de 6% (seis por cento) ao mês. A cota de amortização será determinada pela divisão de R$ 400.000,00 por 4 períodos, resultando em R$ 100.000,00. O valor dos juros depois de um mês será de R$ 24.000,00, que foi determinado pela multiplicação do valor de R$ 400.000,00 por 6 e pela divisão do produto encontrado por 100. Então, a primeira prestação será o total de R$ 100.000,00 com R$ 24.000,00 de juros, resultando no valor de R$ 124.000,00. Depois de efetuado o pagamento, o saldo devedor terá diminuído em R$ 100.000,00, resultando no valor de R$ 300.000,00.
Depois de um mês, o valor dos juros será de R$ 18.000,00, ou seja, os R$ 300.000,00 restantes de saldo vezes 6 sobre 100. Então, a segunda prestação será o total de R$ 100.000,00 com R$ 18.000,00 de juros, resultando no valor de R$ 118.000,00. Depois de efetuado o pagamento, o saldo devedor terá diminuído em R$ 100.000,00, resultando no valor de R$ 200.000,00.
Após um novo mês, o valor dos juros será de R$ 12.000,00, isto é, R$ 200.000,00 vezes 6 dividido por 100. Então, a terceira prestação será o total de R$ 100.000,00 com R$ 12.000,00 de juros, resultando no valor de R$ 112.000,00. Depois de efetuado o pagamento, o saldo devedor terá diminuído em R$ 100.000,00, resultando no valor de também R$ 100.000,00.
Decorrido um novo mês (último), o valor dos juros será de R$ 6.000,00, resultante da multiplicação de R$ 100.000,00 por 6 sobre 100. Então, a quarta prestação será o total de R$ 100.000,00 com R$ 6.000,00 de juros, resultando no valor de R$ 106.000,00. Depois de efetuado o pagamento, o saldo devedor terá diminuído em R$ 100.000,00, resultando no valor nulo, indicando que o financiamento foi quitado. Observe abaixo o controle operacional do financiamento, com base na convenção que determina o cálculo do financiamento pelo SAC, mediante o quadro tradicional de amortização, onde os juros são calculados sobre o saldo devedor.
Como foi possível notar, a capitalização de juros permaneceu invisível neste quadro de amortização tradicional. O objetivo do mercado, em âmbito mundial, em utilizar esse quadro não tem como meta esconder a capitalização de juros aos tomadores de empréstimo, pois o propósito dele está na facilidade e praticidade de sua montagem, sem a necessidade de uso de recursos técnicos (calculadora eletrônica ou computador), exibindo fielmente e exatamente o valor do saldo devedor a cada mês, por meio de uma estrutura construída com extrema simplicidade, destinada ao público em geral.
Neste artigo, a partir deste momento, analisaremos o SAC por meio de outra ótica, entretanto, antes disso, vale relembrar que, quanto ao anatocismo (aplicação de juros sobre juros) no setor imobiliário, a discussão jurídica nos tribunais também está direcionada a outro sistema de amortização, relativo à aplicação da Tabela Price, ou seja, relativo à utilização da tabela de coeficientes do Sistema Francês de Amortização. O foco da análise, nesse outro sistema, é a existência ou não de juros compostos nos financiamentos por ela gerados por meio de seus coeficientes. Essa discussão antiga, ao longo de décadas, ainda está presente pelo motivo da verdadeira existência de juros sobre juros do ponto de vista matemático, mesmo havendo conjecturas com respeito à definição de “capitalização de juros” sob a ótica do meio jurídico. O quadro de amortização tradicional, que impossibilita a visualização da capitalização de juros, também é utilizado nos financiamentos gerados pela Tabela Price, assim como em todos os casos no mercado, quando os juros são calculados sobre o saldo devedor.
Outro problema, na dinâmica desse assunto, está no fato de que há muito tempo em grande quantidade de casos, onde estão presentes entendimentos também equivocados, já se aplica o SAC em substituição ao sistema da Tabela Price, com o propósito de que o regime de juros simples seja, então, aplicado. Isso acaba sendo um problema, visto que o SAC também capitaliza juros. Equivocadamente muitos alegam que não, dizendo que não existe, em referência a ele, uma fórmula com expoentes que gerariam juros compostos. Outros, então, afirmando que, quando empregado o sistema, pagam-se todos os juros do mês, além da cota de amortização, em todos os períodos até cumprir o prazo total para a liquidação do financiamento. Novamente tem-se a impressão de que cada prestação paga efetivamente todos os juros do mês, tal como ocorre na discussão com respeito ao sistema da Tabela Price.
Nesse sentido, como eu já expliquei em meu outro artigo que trata da Tabela Price, o controle do financiamento distorcendo originalmente o comportamento das variáveis é o motivo do equívoco que afeta centenas de milhares de brasileiros. Vale dizer que operacionalmente pode-se criar, sem problemas, como visto no método exposto no início deste artigo, um financiamento pelo SAC. O modo de calcular o valor da cota de amortização, prestação, juros e saldo devedor segue as características que identificam o sistema, ou seja, segue a mera convenção humana para a determinação dos valores dos campos citados. Entretanto, uma convenção apenas indica um procedimento a ser seguido, isto é, um método. Essa metodologia adotada para o cálculo de cada prestação mensal pelo sistema em questão faz efetivamente o saldo devedor ser nulo após o pagamento da última parcela, porém isso não quer dizer que originalmente ocorra dessa maneira a evolução dos valores de juros e amortização pela perspectiva fundamental matemática, embora esteja ocorrendo corretamente em âmbito operacional ou contábil.
Nele, todos os campos (variáveis) do quadro de amortização possuem a mesma unidade (reais). A partir daí a ciência matemática dá permissão ao mutuário de construir tanto operacionalmente quanto originalmente o demonstrativo de evolução do financiamento, indicando, como dito, precisamente o valor do saldo devedor mês a mês em ambos os casos. Contudo, apenas do ponto de vista original (essencial) se mostra nítida a capitalização de juros no caso, a partir do segundo mês até o final.
Diante da polêmica, defendendo erradamente a não capitalização de juros, alguns utilizam a verdadeira afirmação de que o total em juros pelo SAC é menor em comparação ao obtido pelo sistema da Tabela Price e, nesse pensamento, portanto, esses profissionais equivocados divulgam essa condição elevando-a ao patamar de prova, propondo que o excedente são os juros sobre juros cobrados no sistema ao qual efetuam a comparação. Isso está duplamente incorreto, primeiramente porque os dois sistemas são distintos e, ainda, porque ambos capitalizam juros. O fato de que o total em juros pelo SAC seja menor, em comparação com outro sistema, é fruto da característica de que as prestações no primeiro são decrescentes, maiores nos meses iniciais e menores ao final. No segundo sistema analisado na comparação, sistema da Tabela Price, as prestações sempre possuem igual valor. Assim, no outro sistema, os pagamentos de maior valor no início diminuem “mais rápido” a dívida, gerando menos juros futuros, todavia isso não tem nada a ver com o regime de capitalização empregado.
Pela perspectiva matemática, o saldo devedor nasceu do valor financiado e as prestações nasceram de “parcelas específicas em valores menores”, relativas aos próprios pagamentos, situadas graficamente também na data de assinatura do contrato. Essas “parcelas específicas em valores menores”, em questão, não precisam ser obrigatoriamente calculadas, registradas e divulgadas (prestações antecipadas e, por essa razão, sem juros), mas sempre existem matematicamente em todos os financiamentos, mesmo inexistindo um sistema de amortização a elas associado. A soma de todas as “parcelas específicas em valores menores” é sempre igual ao valor financiado nos casos em que o saldo devedor é quitado quando paga a última prestação.
Em âmbito acadêmico, nas disciplinas conhecidas como Matemática Financeira ou Engenharia Econômica, pertencentes aos cursos de Economia, Administração, Engenharia (entre outros), encontramos com frequência, quando estudamos séries de pagamentos com juros, na teoria e prática, essas “parcelas específicas em valores menores”, de extrema e fundamental importância conceitual, que são chamadas cientificamente de “valores presentes” ou “valores atuais”. Do ponto de vista real e matemático, em uma série qualquer de pagamentos, os juros do saldo devedor foram gerados ao longo do tempo sobre o “principal devido”, isto é, parte ainda a ser paga a cada mês, relativa ao valor financiado, que vai diminuindo com o tempo até desaparecer na quitação. Por outro lado, outros juros foram gerados também sobre os valores presentes, caracterizando o outro prato da balança (a prestação). Assim, deve-se dizer que qualquer sistema de amortização deve ser analisado imparcialmente, respeitada também, sem perder a referência, sua natureza mediante a observação original da evolução do dinheiro acrescido de modo similar em suas duas trilhas: dívida e pagamentos. No caso da utilização do quadro de amortização tradicional, a referência é perdida, o que certamente impossibilita a observação da aplicação de juros sobre juros.
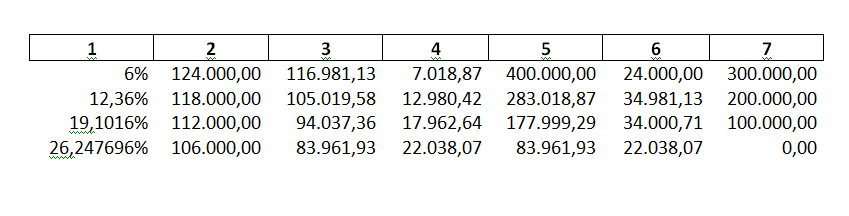
Retornando o nosso pensamento à ótica original, a referência da série de pagamentos, para facilitar, deve ser fixada na data de assinatura do contrato, a origem. Nesse sentido, a critério do observador, a dinâmica de um financiamento pode estar explícita de forma claramente visível, evidenciada de modo justo, abraçada com a realidade, quando, assim, observada em sua origem, isto é, a dívida decrescendo na própria fonte, monitorada em seu ponto inicial. Observe abaixo, o controle original do financiamento, com base nos conceitos fundamentais matemáticos, em se tratando do comportamento das variáveis ao longo do tempo, mediante um quadro alternativo de amortização detalhado com sete campos, por mim estruturado e publicado no ano de 2006. Esse quadro citado é um demonstrativo mensal onde os juros são calculados sobre o principal devido. Note que as porcentagens acumuladas de juros não variam de forma linear, mas, sim, de modo exponencial, caracterizando a incidência de juros sobre juros. Vale dizer que o prazo a e taxa de juros influem nos valores resultantes. Isso foi mencionado por conta do prazo muito reduzido de quatro meses em função da taxa de juros de 6% ao mês.
1 – Porcentagem acumulada de juros (variação exponencial).
2 – Prestação.
3 – Valor presente da prestação = Amortização do principal devido.
4 – Juros sobre o valor presente da prestação.
5 – Principal devido antes de efetuado o pagamento.
6 – Juros sobre o principal devido antes de efetuado o pagamento.
7 – Saldo devedor após efetuado o pagamento.
Nesse quadro acima, é possível notar como originalmente e, não, de modo operacional, a prestação se mostra (ótica fundamental). Sob essa perspectiva, é retratada a realidade do que ocorre com as variáveis do financiamento. O anatocismo, portanto, fica evidenciado a partir da segunda prestação com juros de 12,36% a partir de seu valor presente, ao invés de 12% para o regime de juros simples. A terceira prestação possui juros de 19,1016% a partir de seu valor presente, ao invés de 18% para o regime de juros lineares. A quarta prestação possui juros de 26,247696% a partir de seu valor presente, ao invés de 24% para o regime que não capitaliza juros.
Note que os valores dos pagamentos são os mesmos em ambos os quadros de amortização mostrados neste artigo: R$ 124.000,00; R$ 118.000,00; R$ 112.000,00 e R$ 106.000,00. Isso ocorre também com os saldos devedores: R$ 300.000,00; R$ 200.000,00; R$ 100.000,00 e R$ 0,00. Os totais em juros também são iguais, se os determinarmos a partir dos valores de ambos os quadros: R$ 24.000,00 com R$ 18.000,00 com R$ 12.000,00 e com R$ 6.000,00, resultando em R$ 60.000,00 a partir do quadro operacional (tradicional) e, por sua vez, R$ 7.018,87 com R$ 12.980,42 com R$ 17.962,64 e com R$ 22.038,07, resultando igualmente em R$ 60.000,00 a partir do quadro original. O total amortizado também: R$ 100.000,00 com R$ 100.000,00 com R$ 100.000,00 e com R$ 100.000,00, resultando em R$ 400.000,00 a partir do quadro operacional e, por sua vez, R$ 116.981,13 com R$ 105.019,58 com R$ 94.037,36 e com R$ 83.961,93, resultando igualmente em R$ 400.000,00 a partir do quadro original. Portanto o diferencial está no modo de visualizar o comportamento das variáveis.
Todo financiamento possui um início, um ponto de partida. A única forma de sabermos o que ocorre matematicamente com as variáveis, sob a perspectiva quantitativa e conceitual, de um plano de pagamentos, é não perdendo de vista o ponto de partida. Contudo, infelizmente, controlando de qualquer outro modo o financiamento, perde-se a referência, na medida em que foi deixado de lado o controle original. Assim, nessa trilha, se o controle operacional não retrata o que de fato ocorre, temos, portanto, uma fortíssima tendência para tirar uma conclusão errada (de que não há capitalização de juros), ocorrendo com grande frequência por parte dos mutuários. Essa conclusão equivocada é adotada também por alguns profissionais da área financeira e jurídica. Como especialista no assunto e graduado na área de exatas, onde permanecem os corretos e comprovados fundamentos matemáticos, mergulhados também na rigorosa e exigente esfera acadêmica, posso com propriedade, e absoluta certeza, assegurar que sempre ocorre o seguinte: “todo saldo devedor mensal possui juros e, quando, então, se calcula juros sobre qualquer um deles, conta-se também juros sobre juros, não existindo exceções”. Nesse entendimento, que é o correto sob o ponto de vista matemático, o SAC e o sistema da Tabela Price capitalizam juros, pois esse encargo, quando efetuado o controle, pode ser calculado sobre o saldo devedor a cada mês e o financiamento é efetivamente quitado após o último pagamento, comprovando que o sistema escolhido foi fielmente aplicado, cumprindo o seu objetivo.
Na busca pela única, imutável e absoluta verdade matemática, devemos analisar a situação como de fato ela ocorre, originalmente. Por outro lado, em sua natureza, o homem, dependendo de sua disponibilidade de tempo, das várias opiniões divergentes que o rodeiam, das ferramentas de cálculo a seu dispor, das circunstâncias profissionais e muitas outras condições que o cercam, está sujeito a observar o caso em questão apenas de um único modo, isto é, da forma mais singela. Esse comportamento, sem intenção, às vezes o distancia da realidade. Em outras palavras, alguns métodos matemáticos podem e devem ser criados a fim de gerar praticidade (quadro de amortização tradicional), podendo também ser utilizados e considerados exatos em âmbito operacional ou contábil, uma vez que possuem, no mínimo, parcial respaldo numérico na teoria original, não distorcendo, assim, em nosso exemplo, a importante variável saldo devedor; no entanto, a verdade matemática fundamental relativa a esse assunto nunca pode ser criada, mas, por sua vez, somente descoberta (quadro de amortização original) e, posteriormente, devidamente respeitada por estar correta e possuir integral respaldo numérico e conceitual na teoria original.
Vale dizer que a teoria original matemática para séries de pagamentos com juros, que possibilita a descrição analítica do comportamento do dinheiro em função do tempo, satisfaz e traduz todos os sistemas de amortização operacionais possíveis e ainda permite controlar qualquer sequência de pagamentos de valores aleatórios, não estando esta última, assim, vinculada a nenhum sistema. Como visto, o SAC é apenas um sistema de amortização possível de ser utilizado, assim como outros, tais como: sistema Francês (Price), Alemão, Americano, Misto, Gradiente. Entretanto, a teoria matemática original para séries de pagamentos com juros é o alicerce que permite a construção do “código genético” do financiamento. E por meio desse importantíssimo código, pode-se afirmar, com certeza e clareza, se o plano de pagamentos analisado segue o regime de juros compostos ou simples, entre outras informações.