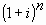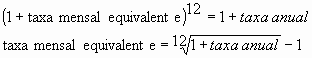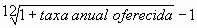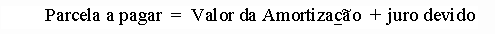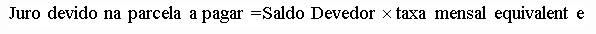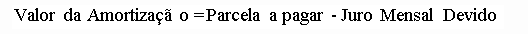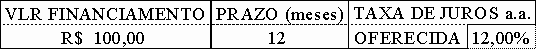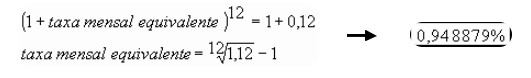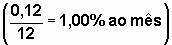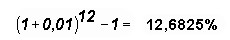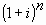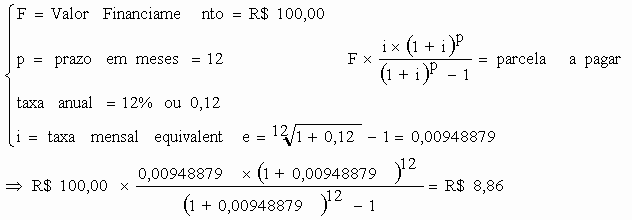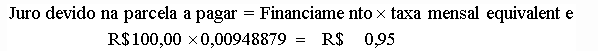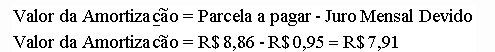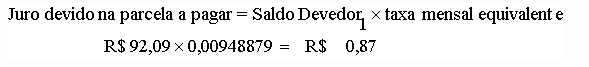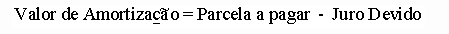1. A questão da taxa de juro anual oferecida, mas na realidade cobra-se outra, maior, denominada "efetiva".
Nos contratos firmados no âmbito do SFH, o sistema de amortização utilizado, na maioria dos casos, é o Sistema Price ou Francês.
O sistema tem por finalidade fornecer o valor da prestação mensal, tendo como base:
valor do Financiamento;
prazo em meses para pagamentos, e
taxa anual de juro pactuada.
O sistema se chama exatamente Price ou Francês, porque fornece uma fórmula em que é possível definir o percentual de juro anual que se deseja pactuar, porém, efetuando pagamentos mensais.
Incorporado às amortizações de empréstimos, pelo matemático inglês Richard Price, no século XVIII, porém, na prática, sendo utilizado primeiramente na França, no século XIX, o sistema é resultado da soma de uma progressão geométrica:
Na própria fórmula temos a expressão
Se o sistema exige a taxa anual de juro, é por isso que se denomina Price, para que se possa pagar, exatamente, a taxa anual de juro que se pactuou, temos que resolver a operação:
.
Ora, os gestores do SFH simplesmente dividem a taxa anual oferecida por 12 meses:
Porém, o correto seria calcular a taxa mensal equivalente:
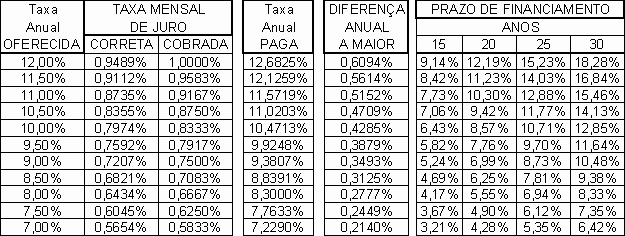
Em termo contratual, tem-se diferença percentual cobrado a maior:
Portanto, num financiamento de 30 anos a uma taxa anual oferecida de 12% ao ano, o mutuário pagaria 18,28% a maior, a título de juro.
Assim, todos os contratos que utilizam o sistema de amortização Price, ficam a mercê dessa distorção, merecendo, portanto, o recalculo da taxa mensal de juro devida, para que se possa ter PRESTAÇÃO e SALDO DEVEDOR, por uma única taxa anual de juro pactuada, conforme determina a Lei, que exige que se defina claramente a taxa de juro pactuada.
2. A questão do anatocismo – o sistema Price de amortização não pratica a cobrança de juros sobre juro.
Outro aspecto do sistema Price, e que muito se tem afirmado, é que o mesmo utiliza a cobrança de juros sobre juro (anatocismo). Isso não tem fundamento.
Calculada a parcela a pagar, pela aplicação da fórmula do Sistema Price, a mesma é constituída de duas partes:
O juro devido na parcela a pagar equivale ao juro mensal sobre o saldo devedor:
A diferença positiva entre a parcela a pagar e o juro mensal devido, amortiza o saldo devedor:
Aonde é que esta a cobrança de juros sobre juro, se o juro mensal é calculado sobre o saldo devedor existente?
Vejamos um exemplo, considerando que a inflação seja nula no período:
Primeiramente, temos que calcular a TAXA MENSAL QUE SE EQUIVALE A TAXA ANUAL OFERECIDA DE 12%:
Na matemática financeira quanto os pagamentos são fixados mensalmente, a taxa de juros também tem que ser. Como o Sistema Price exige que a taxa de juros seja pactuada em termo anual, surge a necessidade de transforma-la em sua equivalente mensal.
Ao se fazer a divisão da taxa anual oferecida (12%) por 12 meses
e aplicá-la na fórmula do Sistema Price, representa em termo anual a taxa de:
Ou seja, maior que a taxa anual oferecida de 12%.
Com a taxa mensal equivalente (0,948879%), isso não ocorre, pois se paga exatamente a taxa anual oferecida
DUAS TAXAS SÃO EQUIVALENTES QUANDO, REFERINDO-SE A PERÍODOS DE TEMPO DIFERENTES, fazem com que um capital produza o mesmo montante, em mesmo intervalo de tempo.
Por exemplo, a taxa de 0,948879% ao mês é equivalente à taxa de 12,00% ao ano, pois um capital colocado a 0,948879% ao mês produz o mesmo montante que produz quando colocado a 12,00% ao ano.
É intrínseco do Sistema Price - que utiliza a soma de uma progressão geométrica, de razão
-, que se a taxa de juro anual oferecida não for corretamente transformada em sua equivalente mensal, paga-se uma taxa de juro maior (EFETIVA).
Saldo Devedor após o pagamento da 1ª parcela:-
Saldo Devedor após o pagamento da 2ª parcela:-
Saldo Devedor após o pagamento da 3ª parcela:-
E, assim, sucessivamente, até a última parcela a pagar.
O Sistema Price de amortização tem uma lógica explicita: do valor da parcela paga, desconta-se o juro mensal sobre o saldo devedor e o restante amortiza a dívida.
Vejamos os pagamentos restantes:
Como é possível afirmar que o Sistema de Amortização Price pratica a cobrança de juros sobre juro?
Afirmar que o Sistema Price de amortização produz cobrança de juros sobre juro é demonstrar conhecimento limitado nessa área de saber.
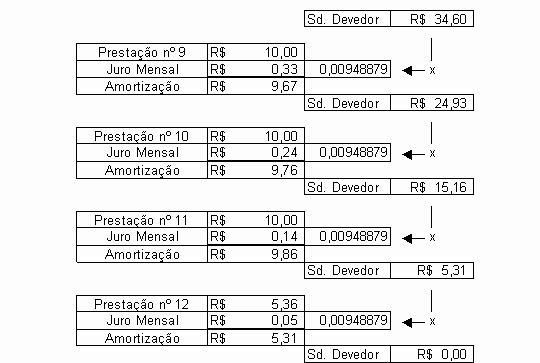
Para demonstrar a lógica do Sistema de Amortização Price, supomos que as parcelas a pagar de nºs 9, 10 e 11, fossem pagas a quantia de R$ 10,00 cada uma, ou seja, valor maior do que a parcela devida (R$ 8,86).
Estaria se pagando algum valor a mais do que o devido? Claro que não.
Vejamos:
Portanto, sendo o saldo devedor a base de cálculo do juro mensal, qualquer pagamento a maior na parcela devida, no referido período, irá amortizar o saldo devedor na mesma proporção do valor excedente. A amortização em excesso, diminui o saldo devedor, assim sendo, na seqüência do plano ocorrerá saldo devedor menor, e, conseqüentemente, o valor do juro mensal, restando quota de amortização à maior.
Notem que os pagamentos a maiores nas parcelas de nºs 9, 10 e 11, vão refletir na última parcela a pagar diminuindo-a de R$ 8,86 para R$ 5,36, no exemplo.
3. A questão de se adicionar ao saldo devedor as amortizações negativas (juros não pagos), sendo que, a legislação proibe a prática do anatocismo.
Somente um ponto ainda é obscuro. Sendo o Sistema Price uma forma de se cobrar os juros anuais pactuados em prestações mensais, objetivando o zeramento da dívida após o pagamento da última prestação, pergunta-se: esse resultado (liquidação do débito) é alcançado quando o Sistema Price é adotado com a incidência da correção monetária?
Eis a questão...
Como o saldo devedor é a base para o cálculo do juro mensal, o que acontece se o saldo devedor aumentar mais que a parcela a pagar?
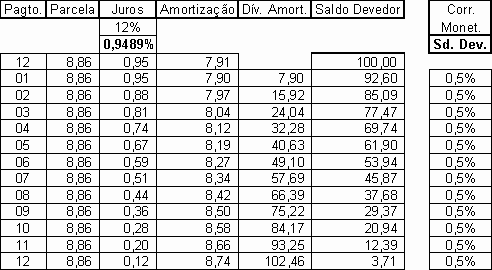
Por exemplo, vejamos o que ocorre:
Ao fim do plano de pagamento resta o saldo devedor de 3,71.
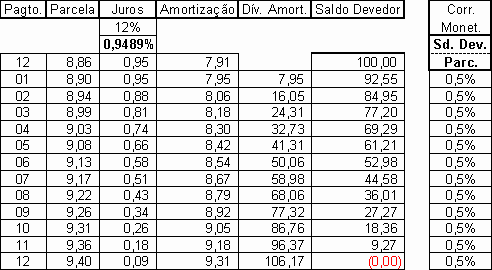
E o que aconteceria se o saldo devedor aumentar na mesma proporção da parcela a pagar?
O saldo devedor é zerado.
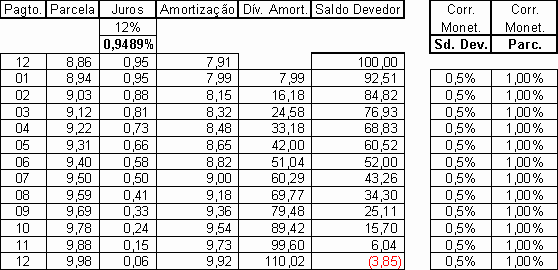
E o que aconteceria se a parcela a pagar aumentar mais que o saldo devedor?
O saldo devedor estaria quitado e ainda sobraria 3,85 de pagamento a maior.
Se a correção no saldo devedor for maior do que a verificada na prestação o contrato não pode se quitado no prazo convencionado.
Eis a lógica da existência do F.C.V.S, porém, extinguiram-no.
Ao estabelecer a primeira parcela através do Sistema Price, o valor resultante, representa todas as parcelas, porém, o juro embutido na parcela, corresponde ao juro simples mensal sobre o Saldo Devedor.
A diferença positiva entre a parcela a pagar e o juro devido, amortiza o saldo devedor:
porém, se ocorrer, que a diferença verificada seja negativa, isso significa que o juro devido é maior do que a parcela paga, e, se essa diferença for adicionado ao saldo devedor, nos próximos cálculos dos juros, ocorrerá o que se denomina anatocismo.
Convencionando prestação, corrigidas por um índice - no caso: (PES/CP)- , e tendo o saldo devedor, correção por outro - índice de atualização monetária da poupança livre - SURGE CONTRADIÇÃO, SE O ÍNDICE DE REAJUSTE DO SALDO DEVEDOR FOR MAIOR QUE O DA PRESTAÇÃO.
Não é possível quitar o empréstimo no prazo convencionado, restando saldo devedor;
Quanto maior a diferença dos índices, dos intervalos de reajustes, a possibilidade de ocorrer anatocismo (juros sobre juro) é evidente.
Se ocorrer o contrário, o financiamento é quitado antes do prazo convencionado.
Portanto, as amortizações negativas (juros não pagos), devem ser controladas a parte, sendo atualizadas pelos mesmos índices aplicados no saldo devedor, mas jamais adicionadas ao saldo devedor, pois isso caracteriza anatocismo.
É o que tenho a comentar.