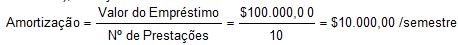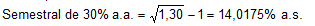A Tabela Price e os efeitos deletérios da capitalização composta de juros

2. DOS SISTEMAS DE AMORTIZAÇÃO.

Uma vez familiarizado com os temas tratados anteriormente, intrinsecamente relacionados à Matemática, é possível passar a considerar a Tabela Price, e como esse instrumento de cálculo de amortizações em financiamentos vem causando polêmica nas mais diversas relações jurídicas.

Contudo, antes de passarmos a essa consideração, nuclear no presente trabalho, passemos a discorrer brevemente sobre os vários sistemas de amortização utilizados nos mais diversos financiamentos no Brasil. Familiarizado com esses sistemas, será possível tratar com mais propriedade da sistemática da Tabela Price.

Com base na maior gama de doutrinas matemáticas, é possível constatar a existência dos seguintes sistemas de amortização:

• Sistema de Pagamento único;

• Sistema de Pagamentos variáveis;

• Sistema Americano;

• Sistema Alemão;

• Sistema Price ou Francês;

• Sistema de Amortização Constante (SAC); e

• Sistema de Amortização Misto (SAM – SAC + Price).

Dos modelos acima retratados, apenas alguns interessam para esse estudo, vez que são de utilização mais ampla nos financiamentos em geral e, basicamente, caracterizam-se pela capitalização composta de juros. Portanto, será dada maior atenção aos seguintes sistemas:

• Sistema de Amortização Constante (SAC);

• Sistema de Amortização Misto (SAM – SAC + Price).

• Sistema Price ou Francês;

Logicamente, por demandar maiores considerações, o sistema francês de amortização, ou Tabela Price, será objeto de análise em momento posterior. Passemos, pois, a considerar as características e peculiaridades de cada um dos sistemas, partindo, pois, da delimitação de um sistema de amortização.

2.1. CONCEITO DE AMORTIZAÇÃO

Segundo o dicionário Houaiss da Língua Portuguesa 4, amortização se define como:

amortização 5

Datação: 1650 cf. DA

Acepções

substantivo feminino

1. ato ou efeito de amortizar(-se)

1.1 Rubrica: contabilidade.

parcela anual retirada pelo proprietário de uma empresa para atender à depreciação de bens ativos (máquinas, equipamentos, móveis etc.)

1.2 Rubrica: economia, termo jurídico.

redução de dívida por meio de pagamento parcial ou gradual acertado entre as partes

1.3 cada um desses pagamentos realizados

Locuções

a. acelerada

Rubrica: economia.

amortização de um ativo (maquinaria, equipamentos etc.) realizada num prazo maior que o de sua vida útil

a. da dívida pública

Rubrica: termo jurídico.

resgate de títulos da dívida pública pelo governo

a. de ações

Rubrica: termo jurídico.

pagamento feito por sociedade anônima ao(s) seu(s) acionista(s) da parte que lhe(s) cabe no acervo líquido da sociedade, implicando a perda do valor patrimonial das ações, enquanto o do capital social permanece intacto

a. negativa

Rubrica: economia.

crescimento do principal de uma dívida que se verifica quando as amortizações (pagamentos) não chegam a cobrir o valor relativo aos juros

a. da dívida pública

Rubrica: termo jurídico.

resgate de títulos da dívida pública pelo governo

a. de ações

Rubrica: termo jurídico.

pagamento feito por sociedade anônima ao(s) seu(s) acionista(s) da parte que lhe(s) cabe no acervo líquido da sociedade, implicando a perda do valor patrimonial das ações, enquanto o do capital social permanece intacto

a. negativa

Rubrica: economia.

crescimento do principal de uma dívida que se verifica quando as amortizações (pagamentos) não chegam a cobrir o valor relativo aos juros

a. de ações

Rubrica: termo jurídico.

pagamento feito por sociedade anônima ao(s) seu(s) acionista(s) da parte que lhe(s) cabe no acervo líquido da sociedade, implicando a perda do valor patrimonial das ações, enquanto o do capital social permanece intacto

a. negativa

Rubrica: economia.

crescimento do principal de uma dívida que se verifica quando as amortizações (pagamentos) não chegam a cobrir o valor relativo aos juros

a. negativa

Rubrica: economia.

crescimento do principal de uma dívida que se verifica quando as amortizações (pagamentos) não chegam a cobrir o valor relativo aos juros

Etimologia

amortizar + -ção; ver mor(t)-

Amortizar significa, portanto, abater o saldo devedor de um determinado capital. A amortização se caracteriza por ato contínuo de minoração de uma obrigação pecuniária.

Assim como define Carlos Patrício Samanez (2004, p. 207):

A amortização é um processo financeiro pelo qual uma dívida ou obrigação é paga progressivamente por meio de parcelas de modo que ao término do prazo estipulado o débito seja liquidado. Essas parcelas ou prestações são a soma de duas partes: a amortização ou devolução do principal emprestado e os juros correspondentes aos saldos do empréstimo ainda não amortizados

PRESTAÇÃO = AMORTIZAÇÃO + JUROS

Essa separação permite discriminar o que representa devolução do principal (amortização) do que representa serviço da dívida (juros). Ela é importante para as necessidades jurídico-tributáveis, têm um efeito fiscal.

O termo carência designa o período que vai desde a data de concessão do empréstimo até a data em que será paga a primeira prestação. Em geral, esse período é negociado entre o credor e o mutuário. Qualquer sistema de amortização pode ter, ou não, prazo de carência.

São, pois, parcelas de trato sucessivo que visam, somadas a remuneração pelo capital envolvido, alcançar a liquidação de operações financeiras por atingir o saldo devedor igual a 0 (zero).

2.2. DO SISTEMA DE AMORTIZAÇÃO CONSTANTE.

Feitas essas breves considerações sobre amortização, passemos, pois, a analisar uma das sistemáticas de amortização de financiamentos, qual seja, o sistema de amortização constante, também conhecido pelo acrônimo SAC.

Tal sistema consiste em um "plano de amortização de uma dívida em prestações periódicas, sucessivas e decrescentes em progressão aritmética (...), em que o valor de cada prestação é composto por uma parcela de juros e outra parcela de capital." (VIEIRA SOBRINHO, 2000, p. 230).

Segundo Samanez (2004, p. 214):

Pelo Sistema de Amortização Constante (SAC), o principal é reembolsado em quotas de amortização iguais. Dessa maneira, diferente da Tabela Price, em que as prestações são iguais, no Sistema SAC as prestações são decrescentes, já que os juros diminuem a cada prestação. A amortização e calculada dividindo-se o valor do principal pelo número de períodos de pagamento. Esse tipo de sistema às vezes é usado pelo Sistema Financeiro de Habitação (SFH), pelos bancos comerciais em seus financiamentos imobiliários e também, em certos casos, em empréstimos às empresas privadas através de entidades governamentais.

Para melhor visualizar a aplicação prática da referida sistematização, poderemos utilizar do exercício proposto pelo professor José Dutra Vieira Sobrinho (2000, p. 230/231), em que se busca elaborar um plano de pagamentos, com base no sistema SAC, correspondente a um empréstimo de $ 100.000,00, à taxa de juros de 3% ao mês, a ser liquidado em 10 prestações mensais, cujo resultado é observado na seguinte tabela:

Observe-se que nesse sistema as prestações são decrescentes, sendo apenas a amortização do capital principal envolvido na operação constantes em função do tempo.

Muito se questiona acerca da legalidade da aplicação do SAC em contratos de financiamentos em geral, sob o argumento de que tal sistematização incorreria em capitalização composta de juros, demonstrado sinônimo de anatocismo, e se incluiria no óbice legal da prática prevista no art. 4º do Dec. 22.626/33.

Embora não seja objeto do presente estudo, vale colacionar decisão oriunda do Egrégio Tribunal de Justiça do Distrito Federal e Territórios sobre o assunto, verbis:

CIVIL E PROCESSO CIVIL. REVISIONAL DE CONTRATO BANCÁRIO. SISTEMA FRANCÊS DE AMORTIZAÇÃO (TABELA PRICE). CAPITALIZAÇÃO MENSAL DE JUROS DEMONSTRADA. DOUTRINA. VEDAÇÃO LEGAL. DECRETO Nº. 22.626/33. ARTIGO 4º. SÚMULA 121 DO STF. ARTIGO 591, CCB/2002. ARTIGO 5º, MP 2.170-35/2001. CONSUMIDOR. PRINCÍPIOS DA TRANSPARÊNCIA E DA INFORMAÇÃO. ARTIGOS 6º, II, 46, 52 E 54, §4º, CDC. SUBSTITUIÇÃO DA TABELA PRICE PELO SAC - SISTEMA DE AMORTIZAÇÃO CONSTANTE. DESCABIMENTO. DOUTRINA. AMORTIZAÇÃO E PRESTAÇÃO. DISTINÇÃO. REGIME DAS RENDAS CERTAS OU DETERMINADAS. ADOÇÃO DO REGIME DA CAPITALIZAÇÃO SIMPLES. CAPITALIZAÇÃO SIMPLES E CAPITALIZAÇÃO COMPOSTA DE JUROS. DISTINÇÃO. COMISSÃO DE PERMANÊNCIA. CUMULAÇÃO COM OUTROS ENCARGOS MORATÓRIOS. ABUSIVIDADE. PRECEDENTES.

(...)

[3] - Igualmente ilícita é a substituição da Tabela Price pelo SAC - Sistema de Amortização Constante (Sistema Hamburguês), que também importa a capitalização composta de juros vedada por lei, vez que o cálculo dos juros incide sobre o salvo devedor.

(...)

(20050111330253APC, Relator CRUZ MACEDO, 4ª Turma Cível, julgado em 07/02/2008, DJ 07/04/2008 p. 92).

2.3. DO SISTEMA DE AMORTIZAÇÃO MISTO

Trata-se de um sistema misto entre o sistema francês de amortização (sistema Price) e o sistema de amortização constante (SAC). Elaborado pelo Banco Nacional de Habitação (BNH), em 1979. Basicamente, consiste num plano de "pagamentos composto por prestações cujos valores são resultantes da média aritmética dos valores das prestações dos planos SAC e Price, correspondente aos respectivos prazos." (VIERIA SOBRINHO, 2008, p. 239). As prestações e juros resultam da aplicação da mesma regra.

Segundo complementa Assaf Neto (2003, p. 365):

O Sistema de Amortização Misto (SAM) foi desenvolvido originalmente para as operações de financiamento do Sistema Financeiro de Habitação. Representa basicamente a média aritmética entre o sistema francês (SAF) ou Price e o sistema de amortização constante (SAC), daí explicando-se a sua denominação. Para cada um dos valores de seu plano de pagamentos, deve-se somar aquelas obtidos pelo SAF com os do SAC e dividir o resultado por dois.

O professor Assaf Neto (2003, p. 351) lança mão de uma tabela exemplificativa, resultante de um exercício em que se propõe a elaboração de um plano de pagamentos com base no sistema de amortização misto, correspondente a um empréstimo de $100.000,00, a uma taxa de 30% ao ano, a ser liquidado em 10 prestações semestrais:

Segundo explica o referido autor (ASSAF NETO, 2003, p. 351):

Conforme foi comentado, o SAC determina que a restituição do principal (capital emprestado) seja efetuada em parcelas iguais. Assim, o valor de cada amortização devida semestralmente é calculada pela simples divisão entre o principal ($ 100.000,00) e o número fixado de prestações (1 semestre), ou seja:

Os pagamentos desses valores determinam, como é natural, decréscimos iguais e constantes no sado devedor em cada um dos períodos, ocasionando ainda reduções nos valores semestrais dos juros e das prestações.

Para o cálculo dos juros trabalhou-se, como é mais comum nessas operações de crédito de médio e longo prazos, com a taxa equivalente composta. Assim, para uma taxa nominal de 30% ao ano, conforme considerada no Exemplo Ilustrativo Geral, a taxa equivalente semestral atinge:

Taxa Equivalente

Os juros, por incidirem sobre o saldo devedor imediatamente anterior, apresentam valores aritmeticamente decrescentes, conforme são apuradas na penúltima coluna do Quadro 12.1. Para o final do primeiro semestre, os encargos financeiros somam: 14,0175% x 100.000,00 = $ 14.017,50; ara o final do segundo semestre: 14.0175% x 90.000,00 = $ 12.615,80; para o final do terceiro semestre: 14,0175% x 80.000,00 = $ 11.214,00; e assim por diante.

Somando-se, para cada período, o valor da amortização do principal com os respectivos encargos financeiros, tem-se o valor da prestação semestral do financiamento. Assim, para o primeiro semestre a prestação atinge: $ 10.00,00 + 14.017,50 = $ 24.017,50;para o segundo semestre: $ 10.000,00 + $ 12.615,80 = $ 22.615,80; e assim sucessivamente.

Pode ser observado, uma vez mais, que a diminuição de $ 1.401,70 no valor dos juros em cada período é explicada pelo fato de as amortizações (fixas) reduzirem o saldo devedor da dívida (base de cálculo dos juros) semestralmente em $ 10.000,00. esta diminuição provoca, em consequência, uma redução nos juros equivalente: 14,017% x $ 10.000,00 = $ 1.401,70.”

Observa-se que esse sistema de amortização é utilizado mais amplamente nos contratos de financiamento imobiliário, principalmente pela Caixa Econômica Federal. Ao que tudo indica, ao utilizar a sistemática da Tabela Price, o sistema de amortização misto incide na prática do anatocismo.

Contudo, trata-se de objeto diverso, sendo que nos limitamos a esclarecer as características principais da sistemática de financiamento mencionada.

2.4. Da tabela price, ou sistema francês de amortização.

O sistema francês de amortização é conhecido no Brasil como Tabela Price, em razão do desenvolvedor da sistematização Richard Price (1723 – 1791), Reverendo Presbiteriano.

Primeiramente, é interessante tecer apontamentos sobre o criador da referida tabela, o contexto histórico em que se encontrava quando da elaboração da sistemática em estudo, e as implicações para que se propunha.

2.4.1. Breve biografia de Richard Price

Richard Price nasceu na Inglaterra, em Tynton, Llangeinor, Glamorgan, em fevereiro de 1723. Filho de Rhys Price, fazendeiro e Ministro Religioso Calvinista de linha extremamente puritana e disciplinador. (NOGUEIRA, 2008, p. 08)

Após a morte de seu pai, em 1740, mudou-se para Londres, para então morar com seu tio Samuel Price, vindo a completar seus estudos na C. Academy, em Tenter Ailey, Moorfields, adquirindo instrução e influência de John Eames, matemático e amigo muito próximo do então falecido Isaac Newton. (NOGUEIRA, 2008, p. 08)

Seguiu seus estudos até 1748, momento em que se formou Ministro Presbiteriano, se tornando capelão de George Streatfiel, sendo que possuía a liberdade de oficiar como Ministro em outras paróquias presbiterianas.

Casou-se com a filha de um arruinado especulador e comerciante do ramo marítimo, Sarah Blundell, em 1758, mesmo ano em que publica uma de suas principais obras, Review of the Principal Questions in Morals, em que propõe a revisão das principais questões morais da época.

Funda, juntamente com Joseph Priestely, Ministro Protestante e descobridor do processo da fotossíntese e da água carbonada, um grupo conhecido por Dissidentes Racionais, e, em 1766, publica Importance of Christianity, obra em que rejeita ideias católicas tradicionais.

Fique sempre informado com o Jus! Receba gratuitamente as atualizações jurídicas em sua caixa de entrada. Inscreva-se agora e não perca as novidades diárias essenciais!

Inscrever

Os boletins são gratuitos. Não enviamos spam. Privacidade

Embora tenha sido mais conhecido como filósofo e teólogo, seus estudos matemáticos vinham de antes das suas publicações de cunho filosófico. Relacionava-se intimamente com Thomas Bayes, expoente do Teorema Fundamental na Estatística, e ministro não-conformista, assim como Price. (NOGUEIRA, 2008, p. 09).

Bayes escreveu, em 1736, um importante artigo, An introduction to the doctrine of flucions, and a defense of the mathematicians agaisnt the objections of the autor of the analyst, e, embora não se conheça seus vínculos acadêmicos, em 1742 foi elevado à condição de companheiro da Sociedade Real Inglesa.

Segundo os biógrafos de Price, após a morte de Bayes, esse encontra um manuscrito intitulado Essay towards solving a problem in the Doctrine of Chances, divulgado em 1763. Até hoje, tal trabalho é conhecido como Teorema de Bayes, influenciador da estatística moderna, que foi conhecido mundialmente graças ao caráter de Price.

Admite-se que Price tenha desenvolvido grande parte de seu conhecimento matemático com Bayes. Vale lembrar, também, que Price produziu a aplicação prática do citado Teorema de Bayes no campo atuarial, vez que haviam falhado em combinar tabelas de mortalidade com anuidades ou pagamentos parcelados. (NOGUEIRA, 2008, p.10)

Em 1769, Richard Price elaborou famosa obra de estatística para o ramo de seguros, Northampton Mortality Tables, a pedido da Equitable Society da Inglaterra. (NOGUEIRA, 2008, p.10)

Segundo José Jorge Meschiatti Nogueira (2008, p. 10):

A partir desse estudo e da elaboração das tabelas de mortalidade, em 1771 seria publicada a obra final sobre o assunto, que viria a ser editada até 1812, sob o título Observations on Reversionary Payments (Observação sobre Devolução de Pagamentos Reversíveis). Nessa obra, Price explica os esquemas de provisão de anuidades a viúvas e idosos, o método para o cálculo dos valores de seguros de vida, a dívida interna, ensaios sobre aritmética e diferentes assuntos na doutrina de rendas vitalícias e, principalmente, a coleção das "Tabelas de Juro Composto", batizada no Brasil como Tabela Price, como já explicado.

É nessa obra que Price expõe seu conceito e seu método utilizado no sistema de pagamentos periódicos com direito a remuneração em benefícios, ou seja, para se calcular o valor de uma série uniforme de pagamentos consecutivos e durante um certo tempo, para receber uma remuneração futura pelo pagamento de rendas certas, em aposentadoria e seguros. Confecciona também a fórmula que produz a recuperação do Capital, a "Juro Composto", que é a mesma coisa que juros sobre juro pelo sistema de pagamentos parcelado. Por ela, pode-se comparar e notar que o prestamista detentor do Capital terá recebido no final, pelo sistema de pagamento, na aplicação de um Capital do mesmo valor, a "Juro Composto" (juro sobre juro), que neste caso e ao final produzirá os mesmos efeitos, com os mesmos resultados.

O ponto alto para o estudo que se pretende será justamente a publicação da obra Observations on Reversionary Payments, em que Richard Price lança mão de suas Tabelas de Juro Composto, utilizadas até hoje para financiamentos.

Ressalte-se que as Tabelas de Richard Price foram originalmente publicadas com objetivo atuarial, uma vez que eram previstas para o cálculo de benefícios previdenciários e de seguridade social.

O ano de 1789 marca a personalidade de Price como defensor do pensamento liberal. Nesse ano, faz o último de seus controvertidos sermões em que defende a Revolução Francesa, produzindo repercussão na sociedade conservadora inglesa, informando que os ingleses também poderiam destronar um rei caso esse fosse cruel. O Rei George III qualificou-o como ateu, financiando panfletos para seus adversários ideológicos, chegando a ser caricaturado como louco e ateu. (NOGUEIRA, 2008, p. 12)

Price manteve fortes vínculos com colonos norte americanos rebeldes, dentre os quais Benjamin Franklin e Thomas Jefferson, sendo partidário da independência das colônias americanas, o que desagradava a monarquia e os setores conservadores.

Price falece em abril de 1791, com 68 anos de idade (NOGUEIRA, 2008, p. 12).

2.4.2. Contexto histórico da época de Price

As primeiras publicações estatísticas começaram a surgir no final do século XVIII, relativas a população e impostos, dentre outros assuntos. O mercantilismo, acompanhado das grandes explorações além mar, haviam avariado a economia das grandes potências europeias. (NOGUEIRA, 2008)

Quanto às limitações técnicas, e a justificativa de utilização das tabelas de Price até um passado recente, salienta Gilberto Melo 6:

Importante ainda salientar que na época em que foi criada a Tabela Price, no século XVIII, não existiam nem mesmo calculadoras, sendo os cálculos realizados por instrumentos rudimentares que não permitiriam o cálculo exponencial dos juros compostos. Esta tábua de fatores chamada Tabela Price veio possibilitar que os cálculos fossem feitos com simples operações matemáticas, adequadas aos instrumentos disponíveis à época, caso contrário seriam necessárias calculadoras científicas que não existiam àquele tempo.

Para melhor ilustrar a dificuldade do homem médio de se elaborar cálculos financeiros, em 1971, quando cursávamos o primeiro ano de Engenharia na UFMG, somente dois alunos em nossa classe possuíam calculadoras manuais. Todos os outros alunos se utilizavam da régua de cálculo para fazer todos os cálculos, desde os mais simples até os mais complexos. Nesta ocasião já havia o curso de programação Fortran na Escola de Engenharia, mas o computador era único, situado na Reitoria da UFMG, funcionava a cartões perfurados e ocupava parte apreciável da enorme sala onde se localizava.

Com a elaboração da Tabela Price de fatores para diferentes situações de taxas e de prazos possibilitou-se ao leigo o acesso à evolução de sua operação de crédito ou arrendamento mercantil. Em 1970 o Prof. Abelardo de Lima Puccini publicou um livro intitulado "Tabela Price – Impressa em Computador", onde apresentou fatores para taxas de juros variando de 5% a 36% ao ano e prazos de financiamento de um a vinte anos. Até então e ainda por algum tempo consultava-se na Tabela Price os fatores necessários para se fazer os cálculos de financiamentos ou arrendamento mercantil neste sistema. Com a grande disponibilidade, a custos acessíveis, de calculadoras financeiras e computadores pessoais, deixou-se de consultar os referidos fatores e passou-se a usar estes equipamentos, onde se entra com os parâmetros necessários e se obtém imediatamente os valores procurados.

Nesse momento histórico, iniciou-se a famigerada Revolução Industrial, com raízes na Inglaterra. As colônias britânicas situadas na América do Norte lutavam pela liberdade.

A França passava por profundas modificações em razão da eclosão de ideologias liberais, em que se destronavam reis cruéis e buscava-se a implementação de ideais democráticos, influenciados fortemente pelo movimento iluminista que movia a burguesia à ascensão.

Economicamente, Adam Smith propunha um modelo de progresso e riqueza. Não eram decretos reais ou leis que equilibravam a oferta e demanda de bens. A força motriz era o egoísmo humano, transmutado de pecado à virtude, resquícios que fomentam a economia até os dias atuais.

Conforme bem salienta José Jorge Meschiatti Nogueira (2002, p. 24):

Era esse modelo de justificação de Adam Smith que iniciava o impulso burguês na corrida pelos lucros. Nele a trilogia liberdade, fraternidade e igualdade assemelhava-se à transformação de Cinderela, cujo sonho sempre acaba com a volta para o mundo da dura realidade: trabalho com árduas jornadas de 15 horas, sem o relativo aumento dos salários, nenhuma segurança e exploração infantil. Nascia o Capitalismo!

É na seguinte frase que podemos resumir esta realidade:

"para formar a sociedade Feliz..., é necessário que grande número de pessoas continue a ser Ignorante e Pobre." (Bemard Mandeville, séc. XVIII)

Daí podemos mensurar as revoluções ocorridas e contextualizadas na época do Reverendo Price, bem como a ilusão causada por alguns dos ideais "libertadores" que, por fim, trariam duras agruras, principalmente para as classes menos favorecidas, e, consequentemente, hipossuficientes.

2.4.3. Conceituação do sistema francês de amortização, ou Tabela Price

A Tabela Price, ou sistema francês de amortização, consiste em um plano de amortização de uma dívida em prestações periódicas, iguais e sucessivas, dentro de um conceito de termos vencidos, em que o valor de cada prestação, ou pagamento, é composto por duas parcelas distintas, a saber, juros e capital, que configura a amortização da dívida originária. (VIERA SOBRINHO, 2000, p. 220/221).

Não necessariamente o sistema em questão implica em prestações mensais, podendo ser em qualquer período de tempo (trimestral, semestral, anual) e ser elaborado com base em qualquer taxa de juros, não se limitando a 1% ao mês.

Segundo José Dutra Vieira Sobrinho (2000, p. 221), o valor das prestações é determinado utilizando-se a mesma fórmula para séries de pagamento com termos vencidos, qual seja:

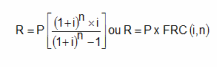
Sendo “P” o principal capital; “i” a taxa de juros,”n” o prazo considerado exponencialmente, e “R” as parcelas (em igual valor).

Como ensina o citado autor (VIEIRA SOBRINHO, 2000, p. 221)

A parcela de juros é obtida multiplicando-se a taxa de juros (mensal, semestral ou anual) pelo saldo devedor existente no período imediatamente anterior (mês, trimestre, semestre ou ano). A parcela de amortização é determinada pela diferença entre o valor da prestação e o valor da parcela de juros. Assim, o valor da parcela de juros referente à primeira prestação de uma série de pagamentos mensais é igual à taxa mensal multiplicada pelo valor do capital emprestado ou financiado (que é o saldo devedor inicial).

Para melhor visualização do funcionamento da referida tabela, o Professor José Dutra Vieira Sobrinho utiliza um exemplo ilustrativo didático, em que se propõe o cálculo das parcelas de juros e amortização referentes a primeira prestação, de um empréstimo de $ 8.530,20, à taxa de 3% ao mês, para ser liquidado em 10 prestações iguais. Eis a resolução do problema proposto (VIEIRA SOBRINHO, 2000, p. 221/222):

“a) Valor da prestação

R = P x FRC (i, n) = 8.530,20 x FRC (3%, 10)

R = 8.530,20 x 011723 = 1.000

b) Valor da parcela de juros (J)

J = i x P = 0,03 x 8.530,20 = 255,91

c) Valor da parcela de amortização (A)

A = R – J = 1.000– 255.91 = 744,09”

Para que possamos determinar as parcelas de juros e as parcelas de amortizações correspondentes às demais prestações, é necessário convencionar o seguinte:

Jt = parcela de juros referente ao período de ordem t (t = 1, 2, 3, ..., n)

At = parcela de amortização referente à prestação de ordem t (t = 1, 2, 3, ..., n)

Pt = Saldo devedor referente ao período de ordem t (t = 1, 2, 3, ..., n - 1)

Assim, o valor da parcela de juros referente à primeira prestação será representado por J1, da segunda por J2, da quinta por J5, e assim sucessivamente; idem para as parcelas de amortização. Quanto ao saldo devedor, o saldo inicial será representado por P0; o saldo devedor no final do primeiro período após a dedução da primeira amortização (A1) será representado por P1; o saldo devedor no final do segundo período após a dedução da segunda amortização (A2) será representado por P2. e assim por diante.

Voltemos ao exemplo em pauta para calcular as parcelas de juros e amortização referente à segunda prestação.

J2 = i x P1

P1 = P0 – A1 = 8.530,20 – 744,09 = 7.786,11

J2 = 0,03 x 7.786,11 = 233,58

A2 = R – J2 = 1.000– 233,58 = 766,42

Para a terceira prestação:

J3 = i x P2

P2 = P1 – A2 = 7.786,11 – 766,42 = 7.019,69

J3 = 0,03 x 7.019,69 = 210,59

Operando da mesma forma para as demais prestações, teremos os valores resumidos na Tabela 8.1 para a série de 10 prestações, que vamos denominar plano de pagamento do empréstimo.

Dado o exemplo acima, o ilustre professor demonstra de forma muito minuciosa como se dá a aplicação da Tabela Price em financiamentos. Da operação em questão, surge uma tabela a fim de se visualizar o plano de pagamentos, que se transcreve abaixo (VIERA SOBRINHO, 2000, p. 220/221):

Por fim, é interessante a comparação efetuada por Alexandre Assaf Neto (2003, p. 366/367), entre os três sistemas de amortização considerados, levando-se em consideração uma operação de $ 100.000,00, com uma taxa de juros de 30% ao ano, a ser liquidada em 5 anos, em 10 prestações semestrais, cujo resultado, levando-se em conta as fórmulas utilizadas para cada sistema de amortização, resulta nas tabelas seguintes:

Sistema de Amortização Constante (SAC)

Sistema Francês de Amortização (Tabela Price)

Sistema de Amortização Misto (SAM)

É possível observar, de forma clara e sem maiores complicações, que, de todos os sistemas de amortização, a sistemática da Tabela Price apresenta maior onerosidade ao devedor. No Sistema de Amortização Constante, tomando o exemplo citado, o total de juros da operação é de $ 77.096,50, enquanto no Sistema de Amortização Misto $ 84.470,80, e, por fim, pela Tabela Price $ 91.844.

A diferença da Tabela Price em razão do sistema SAC é de $ 14.747,50, e em função do Sistema Misto de Amortização é de $ 7.373,20. As diferenças são maiores ainda quando a prestação se estende ao longo de um prazo mais elastecido, haja vista os juros comportarem-se de forma exponencial em função do tempo, e não de forma linear.

Aos olhos leigos, característica da grande maioria populacional que possui financiamentos em instituições financeiras que utilizam a Tabela Price, os juros, por si só, são abusivos. Contudo, ultrapassado o primeiro momento de surpresa, é possível observar outros abusos constantes da sistemática Price de capitalização composta de juros, mormente em razão da prática do anatocismo, o que se verá adiante.

2.5. A TABELA PRICE E A QUESTÃO DA CAPITALIZAÇÃO COMPOSTA DE JUROS (ANATOCISMO)

Segundo Luiz Antonio Scavone Júnior (2007, p. 195), a Tabela Price, também conhecida como sistema francês de amortização, "pode ser definida como o sistema em que, a partir do conceito de juros compostos (juros sobre juros), elabora-se um plano de amortização do capital em parcelas periódicas, iguais e sucessivas, considerando o termo vencido."

Segundo ainda o referido autor:

Com fundamento em Mário Geraldo Pereira (tese de doutorado), ensina José Dutra Vieira Sobrinho "que a denominação tabela price se deve ao matemático, filósofo e teólogo inglês Richard Price, que viveu no século XVIII e que incorporou a teoria dos juros compostos às amortizações de empréstimos (ou financiamentos). A denominação ´´sistema francês´´, de acordo com o autor citado, deve-se ao fato de o mesmo ter-se efetivamente desenvolvido na França, no Século XIX. Esse sistema consiste em um plano de amortização de uma dívida em prestações periódicas, iguais e sucessivas, dentro do conceito de termos vencidos, em que o valor de cada prestação, ou pagamento, é composto por duas parcelas distintas: uma de juros e uma de capital (chamada amortização). (PEREIRA, 1965, p 176 apud SCAVONE JÚNIOR, 2007, p. 195)

Nesse sistema de amortização as parcelas são compostas de um valor referente aos juros, calculado sobre o saldo devedor amortizado, e outro referente a própria amortização.

Os juros são compostos na exata medida em que, sobre o saldo amortizado, é calculado o novo saldo, com base nos juros sobre aquele aplicados, e, sobre este novo saldo amortizado, mais uma vez os juros sobre todo o capital e não sobre a parcela devida, e assim por diante. (SCAVONE JÚNIOR, 2007, p. 195/196)

Portanto, observa-se que a Tabela Price, por natureza, é construída com base em tabelas preexistentes de juro composto.

Mais uma vez, vale frisar que, conforme demonstrado, para os efeitos jurídicos, capitalização composta de juros implica, necessariamente, em anatocismo, uma vez que são palavras sinônimas utilizadas em diferentes ciências.

Frente a outros sistemas de amortização, parece ser mais vantajosa, uma vez que as parcelas são invariáveis, periódicas e sucessivas, o que normalmente não ocorre com outras tabelas de financiamento.

Para chegar a essa conclusão, faz-se necessário ir ao âmago da questão, utilizando-se da publicação dos manuscritos do próprio Richard Price a fim de aferir se há ou não capitalização de juros, ou anatocismo, em sua sistemática de amortização de dívidas. Como, certamente, esbarra-se no óbice da indisponibilidade de tamanha preciosidade, é satisfatório saber que o já citado professor José Jorge Meschiatti Nogueira (2008, 27-47) traz em sua obra trechos das traduções juramentados do livro Observations on Reversionary Payments, em que Price publica suas tabelas.

Nesses livros, é possível confirmar que o próprio Price, faz menção às suas tabelas como capitalização composta de juros, até mesmo batizando-as de tabelas de Juro Composto. Passemos, pois, a analisar a construção das tabelas pelo próprio Price, ressaltando que as traduções juramentadas reproduzidas por Nogueira, e colacionadas no presente trabalho, foram encomendadas por ele e registradas no 2º Registro de Títulos e Documentos de Campinas, por microfilme sob o n.º 119.798, literalmente:

CONSTRUÇÃO das quatro tabelas precedentes

ESTAS Tabelas podem ser encontradas na maioria dos livros que tratam de Juro Composto e anuidades; mas tem sido, neste estudo, tantas vezes necessário consultá-las, que foi preciso poupar o leitor o trabalho de recorrer a outros livros por causa delas.

O 1º, 2º, 3º, &c. números na primeira tabela correspondem aos quocientes de unidade divididos pela 1ª, 2ª, 3ª &c. potências respectivamente de £1 acrescida de seu juro para um ano; ou 1.023, 1.025, 1.03, 1.035, 1.04, 1.05, &c. de acordo com o juro correspondente de 2, 2 ½, 3, 3 ½, 4, 5, &c. por cento.

O 2º, 3º, 4º &c. números na segunda tabela correspondem às somas do 1º e 2º; do 1º, 2º e 3º; do 1º, 2º, 3º e 4º, &c. &c. números respectivamente na primeira Tabela.

Os números na 3ª Tabela correspondem às potências de £1 acrecidas do seu juro para um ano. Ou seja, r, r2 r3, &c.

o 2º, 3º, 4º &c. números na segunda tabela correspondem às somas do 1º e 2º; do 1º, 2º e 3º; do 1º, 2º, 3º e 4º, &c. números da 3ª Tabela, acrescidos da unidade. (PRICE, 1803, p. 286. apud NOGUEIRA, 2007, p. 28).

Primeiramente, podemos observar às claras, que o próprio Richard Price admite que suas tabelas são construídas com Juro Composto, o que vimos tratar-se de anatocismo, sendo sinônimos.

Expõe-se abaixo sistemática de construção das tabelas de juro composto confeccionada por Richard Price, conforme notas explicativas (PRICE, 1803 apud NOGUEIRA, 2007, p. 30/33.

Tabela I

O presente Valor (Valor Presente) de £1 a ser recebido ao final de qualquer número de Anos, não excedendo a 100; descontado a Taxas de 2, 2 ½, 3, 3 ½. 4, 4 ½, 5, 6, 7, 8, 9 e 10 porcento de Juro Composto.

(...)

Tabela II

O valor Presente da Anuidade sobre Uma Libra qualquer Número de Anos não excedendo a cem.

(...)

Tabela III

Mostra a quantia a qual o Capital de £1 crescerá a Juro Composto em qualquer Número de Anos não excedendo a cem.

(...)

Tabela IV

Mostra a Quantia a qual £1 anual crescerá a Juro Composto em qualquer número de Anos não excedendo a cem. (PRICE, 1803, p. 262, 263 apud NOGUEIRA, 2007, p. 30, 32).

É fácil ver que, por questão de nomenclatura, Price atribui a todas as suas tabelas a sistemática de juros compostos. Portanto, sob esse enfoque, é inquestionável a capitalização composto de juros, ou anatocismo conforme observado, nas tabelas de remuneração de capital do Reverendo Price.

Mais interessante ainda, sob esse argumento, é observar a forma didática em que Price (1803, p.287 apud NOGUEIRA, 2007, p. 34/36) explica a utilização de suas tabelas de juro composto na forma de perguntas e respostas, que passa-se a transcrever:

Questão I – A que montante ou anuidade uma determinada quantia ou anuidade aumentará, em um determinado número de anos, a uma determinada taxa de Juro Composto?

Resposta. Multiplique o número na 3ª Tabela, referente a determinada taxa e contrário ao determinado número de anos, pela determinada quantia ou anuidade, e o produto obtido será a resposta.

Exemplo. O produto de £40 em 2.0258 (ou seja, £81.032) corresponde ao montante ao qual o Capital de £40 crescerá em 18 anos, considerando- se o juro a 4 por cento; e o mesmo produto corresponde igualmente à anuidade a qual uma anuidade de £40 crescerá no mesmo período, considerando-se o mesmo juro.

(...)

Questão II – A que montante uma determinada anuidade equivalerá a uma determinada taxa de Juro Composto por um determinado número de anos?

Resposta: Multiplique o numera na quarta Tabela, referente à taxa e contrário ao determinado número de anos, pela determinada anuidade, e o produto obtido será a resposta.

Exemplo. O produto de £40 em 25.6454 (ou seja, £1025.826) corresponde ao montante ao qual £40 anuais equivalerão em 18 anos, considerando-se o juro a 4 por cento.

(...)

Questão VIII - Admitindo-se que o esquema de uma sociedade para concessão de anuidades a viúvas seja tal que, caso um membro viva um ano após sua admissão, sua viúva terá direito a uma renda vitalícia de £20. No caso de sete anos, a mais £10, ou £30 no total. No caso de quinze anos, a um outro adicional de £10, ou £40 ao todo. Quais deveriam ser os pagamentos anuais dos membros com idades de 30, 40 e 50 anos, supondo-se que eles tenham a mesma idade que suas esposas, e considerando-se o Juro Composto a 4 por cento?

Resposta: De acordo com a hipótese, explicada na p. 2, e portanto, muito próximo, de acordo com as Tabelas de Observação para Breslaw e Norwich, ou Tabelas V e VIII no início do Vol. II:

£8.44; £8.69; £9.05.

Mais uma vez, percebe-se que o próprio Richard Price denomina suas tabelas como de juros composto.

Portanto, pela leitura do livro Observations on Reversionary Payments é possível visualizar perguntas e respostas em que Price explica o uso das tabelas, que ele mesmo denomina de juros composto.

Não bastassem os argumentos pelo próprio Price, é possível observar a questão da capitalização composta de juros em suas tabelas da leitura de várias doutrinas Matemáticas, dentre as quais, pode-se citar:

14. Amortização a Juros Compostos

14.1 Método francês ou de amortização progressiva

Por esse método, pelo qual as prestações destinadas à amortização da dívida são periódicas e constantes, os juros incidem somente sobre o saldo devedor, no final de cada período. A prestação empregada na amortização gradual da dívida compreende duas parcelas variáveis, segundo lei conhecida, cujas somas porém são: uma constante, crescente, destinada à amortização do capital, e a outra, decrescente, destinada à cobertura dos juros. (grifos não constam do original) (CAVALEIRO, 1992, p. 137)

O sistema price consiste em colocar um capital a juros compostos capitalizados mensalmente a uma taxa anual (FRANCISCO, 1976, p 44 apud SACAVONE JÙNIOR, 2007, p. 196)

A tabela Price já teve grande aceitação no mercado brasileiro e ainda é utilizada atualmente, principalmente nos financiamentos imobiliários. A sua grande característica é ter a taxa nominal como elemento de entrada, ao passo que os fatores são calculados com a taxa efetiva dela decorrente. Por exemplo, uma tabela com a taxa nominal de 36% ao ano capitalizados mensalmente terá as seguintes características:

(...)

Conforme visto no problema anterior, a taxa efetiva anual é de 42,58 %, muito maior que a taxa nominal de 36% ao ano. Assim, muito cuidado deve ser tomado com a tabela price, pois a taxa nominal de juros de cada tabela é sempre menor do que a taxa efetiva anual correspondente, podendo essa diferença alcançar valores bastante significativos. (PUCCINI, 1999, p. 74)

Devido ao fato de ser bastante usual financiamentos a longo prazo, considerando-se taxas anuais com capitalização mensal a serem resgatados ao longo de anos por meio de prestações mensais, resolveu-se tabelar a fórmula, para diversos valores de juros e de capital, de tal modo que tivéssemos o valor da prestação correspondente ao caso do empréstimo de um capital unitário. Tais tabelas são denominadas Tabelas Price. (FARO, 1998, p. 74. apud SCAVONE JÚNIOR, 2007, p.214)

É possível observar que as condições díspares da Tabela Price são objeto de cautela até mesmo entre os doutrinadores, uma vez que lhe é reconhecida que a taxa efetivamente cobrada supera a taxa nominal prevista contratualmente.

Ainda, pode-se acrescentar a perícia noticiada por Luiz Antônio Scavone Júnior (2007, p. 210/212), nos autos do processo 418/96, que tramitou perante a 8ª Vara Cível de Aracaju – SE, nos seguintes termos:

"Queira o Sr. Perito informar se a metodologia price, bem como qualquer tipo de metodologia de cálculo que se utilize juros compostos, prestigiam a contagem de ‘juros sobre juros’. Justifique a resposta."

"Resposta: À guisa de intróito, afigura-se-nos de bom alvitre trazer a lume algumas observações conceituais sobre o ‘sistema price’, resgatadas do já mencionado livro Matemática financeira objetiva e aplicada, de Abelardo de Lima Puccini, e da apostila Curso de matemática financeira básica, que editamos em junho de 1996:

Sistema price: Série Uniforme (Prestações Iguais)

1.1 Considerações Preliminares

Bastante difundido nos meios comerciais brasileiros, o sistema price tem por característica primordial a igualdade absoluta do valor monetário de suas prestações, nas quais se enclausuram, além das verbas amortizadoras do principal financiado, os juros cobrados pelos agentes emprestadores.

Constitui-se, deste modo, relação fundamental do modelo em estudo: Prestação = Amortização + Juros.

Para a obtenção dos valores relativos a cada uma das parcelas integrantes da precitada relação, deve-se observar, com rigor científico, a seguinte sequencial:

a) em primeiro lugar, calcula-se o valor da prestação constante, podendo –se, para tanto, contar com o auxílio da calculadora financeira HP-12C;

b) a seguir, efetua-se o cálculo dos juros do período , aplicando-se a taxa contratual sobre o saldo devedor acumulado (montante) existente no início do período correspondente;

c) por fim, calcula-se o valor da amortização do principal financiado, ou seja, a diferença entre o valor da prestação constante (a) e o valor dos juros do período (b).

Com o passar do tempo, ao passo em que o valor dos juros vai decrescendo gradativamente,as amortizações, inverso modo vão se tomando cada sempre resulte no valor da prestação constante (...).

Sistema price: Série Uniforme (Prestações Iguais)

1.2 Propriedades

O exemplo acima permite-nos, também deduzir as duas propriedades essenciais do sistema price:

• qualquer termo da amortização é igual ao seu antecedente multiplicado por (1 + i);

• o saldo devedor remanescente será sempre o valor presente das prestações vincendas.

É de todo proveitoso que se confira a exatidão das propriedades enunciadas, empregando-se, para tanto, os valores constantes da tabela acima.

Rememoremos os postulados básicos que informam o modelo francês de amortização, a conhecida tabela price e passemos à questão nuclear que motivou a formulação do quesito em análise, qual seja, se a metodologia price, bem como qualquer tipo de metodologia de cálculo que se utilize de juros compostos, prestigiam a contagem de juros sobre juros (...).

O que até aqui dissemos já permite depreender ser afirmativa a resposta deste vistor, na medida em que, quer no bojo do sistema price, em particular, quer no das demais hipóteses metodológicas especuladas, a base de cálculo sobre o qual incidirá a taxa de juros será sempre o saldo da principal acrescido dos juros acumulados ate o período imediatamente anterior, em síntese, o montante.

Em acréscimo, relembramos que nos domínios da Matemática Financeira a capitalização composta de juros (contagem de juros sobre juros) se verifica sempre que se emprega fórmula onde se embute a expressão (1 + i)n, por isso mesmo denominada de fator de capitalização ou fator de acumulação de capital, cabendo, por oportuno, reavivar que:

a) o dinheiro cresce mais rapidamente a juros compostos do que a juros simples;

b) a juros compostos o dinheiro cresce exponencialmente e em progressão geométrica ao longo do tempo;

c) em síntese: no regime de juros simples tem-se como base de cálculo o principal; no de juros compostos, o montante.

No âmbito do modelo price, especificamente, a capitalização de juros se faz incontroversa quando se contempla a fórmula utilizada para o cálculo das prestações constantes da série postecipada, dentro da qual se encastela, sem nenhum pudor, o fator exponencial (1 + i)n." (grifos não constam do original)

Portanto, sendo o juiz, na maioria das vezes, leigo nas questões matemáticas, utiliza-se de expert no assunto a fim de suprir esse déficit, o que implica na resolução da matéria fática.

Nesse passo, verifica-se que o perito supramencionado põe fim a discussão afirmando que a sistemática Price capitaliza efetivamente juros da forma composta, cerne da discussão nos autos mencionados.

Para não restar dúvidas, convêm ainda colacionar tabela explicativa, em mínimos detalhes, do professor Luiz Antônio Scavone Júnior (2007, p. 207/208), através de um exemplo que consiste em calcular o financiamento de R$ 11.255,08, a ser pago em 12 (doze) parcelas mensais e consecutivas, com juros de 1% ao mês de acordo com a Tabela Price, cujo resultado são parcelas de R$ 1.000,00.

Conforme salienta o próprio autor (SCAVONE JÚNIOR, 2007, p. 207/208):

Pelo que se observa, os R$ 11.255,08 iniciais transformaram-se em R$ 12.000,00. Pagou-se, assim, R$ 744,92 de juros.

Com efeito, na coluna da direita é possível visualizar perfeitamente os juros aplicados uns sobre os outros, vez que sempre incidentes sobre o novo valor de capital, antes da amortização que, aliás, não representa uma parcela igual ao capital em razão do prazo, restando parcela extra de capital para incidência de novos juros. A título de comparação, imaginemos a cisão do capital em várias parcelas iguais, sobre as quais é aplicada a fórmula para cálculo do montante, de acordo com a fórmula para cálculo do montante, de acordo com a fórmula que aplica capitalização simples, ou seja: "S = P x (1 + i x n)", na qual P – Principal; i = taxa de juros; n = prazo; S = valor futuro; para o mesmo valor e prazo e cada parcela representada por um doze avos do capital inicial, as parcelas com vencimentos mais distantes teriam juros maiores em razão do prazo estipulado para a devolução da parcela de capital correspondente e o resultado é o que segue:

Portanto, nesse pequeno exemplo, usando a tabela price, o devedor pagaria R$ 744,92 de juros, e, ao revés, utilizando juros simples sobre cada parcela de capital, o pagamento seria menor, ou seja, R$ 731,55.

Reforçando os argumentos econômicos de que a Tabela Price capitaliza juros de forma composta, Scavone Júnior (2007, p. 208/210), sustenta que é possível visualizar tal prática na medida em que se aplica o "fator de valor atual" (FVA) a cada parcela obtida pela sistemática da Tabela Price. Tal aplicação gera um resultado que, somados, indicam o valor do capital inicial. O FVA e encontrado tomando-se a termo a seguinte fórmula:

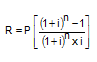
Em que P = principal; i = a taxa de juros; n = o prazo; e R = prestações. A fórmula aplicada inversamente resulta em valor idêntico ao da prestação apurada pela Tabela Price, o que comprova a aplicação de juros compostos para esse sistema.

Para facilitar essa visualização, dispomos do exemplo do citado autor, com base em estudo da obra de José Dutra Vieira Sobrinho (Scavone Júnior, 2007, p. 209/210), assim descrito:

“Nesse sentido, aplicando o FVA (fator de valor atual) de acordo com os juros capitalizados de forma composta às prestações apuradas pelo sistema francês, no mesmo exemplo da nota anterior, com capital inicial de R$ 11.255,08 para pagamento em doze parcelas e juros de 1% ao mês, o resultado obtido é o seguinte:

Prestação	Prestação Valor	Valor presente	Juros mensais %
1	1.000	990,01	1,0%
2	1.000	980,30	1,0%
3	1.000	970,59	1,0%
4	1.000	960,98	1,0%
5	1.000	951,47	1,0%
6	1.000	942,05	1,0%
7	1.000	932,72	1,0%
8	1.000	923,72	1,0%
9	1.000	914,34	1,0%
10	1.000	905,29	1,0%
11	1.000	896,32	1,0%
12	1.000	887,44	1,0%
Soma:	12.000	11.255,23

Tendo em vista que fórmulas matemáticas são abstrações e, por conseguinte, requerem comprovação, podemos utilizar a fórmula para obtenção do montante pela sistemática dos juros compostos, ou seja, S = P x (1 + i)n sobre qualquer dessas parcelas de valor presente, eu o resultado será, exatamente a prestação obtida pelo sistema francês.

(...)

Vejamos, por exemplo, a sexta prestação, cujo valor presente (P) equivale a R$ 942,05. aplicados juros de 1% ao mês (i), pelo prazo de sis meses (n). O resultado, por evidente, será de R$ 1.000,00, ou sejam aquela prestação apurada pelo sistema francês.

Não resta dúvida, assim, que há juros compostos na tabela price.

(grifei)

Por fim, lançando uma pá de cal no assunto, é possível reunir vários eminentes cientistas da Matemática e Economia signatários de manifesto em que se atesta a ocorrência da capitalização composta de juros na Tabela Price, litteris:

DECLARAÇÃO EM DEFESA DE UMA CIÊNCIA MATEMÁTICA E FINANCEIRA 7

Nós, abaixo identificados, professores de matemática financeira, autores de livros e de outros trabalhos sobre essa importante ciência, preocupados com posições equivocadas assumidas por pessoas e entidades, freqüentemente divulgadas pela imprensa ou contidas em laudos periciais envolvendo cálculos financeiros, declaramos que a fórmula utilizada para o cálculo das prestações nos casos de empréstimos ou financiamentos em parcelas iguais, de aplicação generalizada no mundo, e que no Brasil é também conhecida por Tabela Price ou Sistema Francês de Amortização, é construída com base na teoria de juros compostos (ou capitalização composta), sendo a sua demonstração encontrada em todos os livros de matemática financeira adotados nas principais universidades brasileiras.

A capitalização composta é a base dos cálculos utilizados nas operações de empréstimos, financiamentos e seguros, nas aplicações em cadernetas de poupança, títulos públicos e privados, FGTS, fundos de investimentos, fundos de previdência, fundos de pensão, títulos de capitalização e em todos os estudos de viabilidade econômica e financeira realizados no Brasil e nos demais países do mundo. Assim, com base nesse fato incontestável, é imprescindível que a Justiça brasileira faça um reexame das interpretações das leis e decretos que levaram alguns tribunais do nosso país a proibir esse critério de cálculo. E, permanecendo o impasse jurídico, é dever do legislativo votar uma lei que corrija definitivamente esse equívoco histórico.

São Paulo, julho de 2004.

ADEMAR CAMPOS FILHO Professor autônomo - SP

ADEMIR CLEMENTE Professor da UFPR

ALEXANDRE ASSAF NETO Professor da USP

ANTÔNIO CARLOS LOPES Professor da PUC–SP

ANTÔNIO CORDEIRO FILHO Professor da PUC–SP

ARMANDO JOSÉ TOSI Professor autônomo - SP

CARLOS ROBERTO VIEIRA ARAÚJO Professor da UNIFEI–SP

CLÓVIS DE FARO Professor da FGV-RJ

JOSÉ DUTRA VIEIRA SOBRINHO Professor autônomo - SP

JOSÉ NICOLAU POMPEO Professor da PUC-SP, da USP e da Fundação Santo André

JOSÉ MARIA GOMES Professor autônomo - SP

SAMUEL HAZZAN Professor da FGV e da PUC-SP

UDIBERT REINOLDO BAUER Professor da FURB-SC

WALTER DE FRANCISCO Ex-Prof. da Univ. Metodista de Piracicaba (SP) - UNIMEP

WASHINGTON FRANCO MATHIAS Professor da USP

WILSON VILANOVA Professor da PUC - SP

Portanto, impossível tentar divergir da irrefutável prova matemática da capitalização de juros ocorrida nos financiamentos construídos com base na Tabela Price.

Outro aspecto interessante de se observar na dita sistemática é o fato de os juros incidirem antes da amortização. Tal prática implica na antecipação da cobrança de juros, o que, por si só, desvirtua o caráter acessório desse. Desta forma, os juros são cobrados antes do vencimento do capital, e, numa primeira análise, constitui, ao menos, no enriquecimento ilícito do credor, sem se falar nas terríveis consequências de se onerar o devedor além do devido.

Nesse sentido, discursam os professores Luiz Antônio Scavone Júnior e Pedro Afonso Gomes 8 (2000):

O artifício utilizado pelos credores para mascarar a prática do anatocismo é, na tabela price, fazer com que os juros "desapareçam" do total da dívida, cobrando-os na parcela vencida. Ocorre que os juros não são exigíveis mês a mês sobre o débito integral, porque parcelas de capital ainda se vencerão. A tabela price antecipa os juros vincendos, de forma a onerar mais o mutuário

Portanto, em análise aos doutrinadores que procederam ao estudo Técnico da sistemática Price de amortização de empréstimos e financiamentos podemos chegar a conclusões lógicas, quais sejam, de que a referida Tabela capitaliza juros de forma composta e que possui artifícios que desnaturam os juros tal qual acessório, imprimindo-lhes o caráter de obrigação principal.

Para estimular ainda mais a discussão, faz-se necessário, antes mesmo de proceder ao estudo jurídico da Tabela Price colacionar declaração entusiasta do próprio Richard Price, acerca da remuneração do capital pela sistemática composta de capitalização de juros:

"Um penny posto a juros capitalizados do dia do nascimento de nosso Salvador a cinco per cent, até 1781, produz um crescimento equivalente à duzentos milhões de globos de outro sólido, iguais ao do tamanho da terra. Mas se fosse posto a juros simples, no mesmo período, produziria uma quantia igual ou não maior do que sete shilings e seis pences" 09 (SCAVONE JÚNIOR, 2007, p. 214)

Nesse passo, passemos, pois a analisar as implicações jurídicas que orbitam a prática da capitalização composta de juros, especificamente na Tabela Price. É importante ressaltar que essas questões transcendem qualquer fria discussão oscilante entre legalidade e ilegalidade.

Mais do que isso, a capitalização composta de juros influi diretamente na vida de incontáveis brasileiros que se valem unicamente de instrumentos de concessão de crédito para alcançar uma vida digna em vários aspectos.

Registrado, à analise jurídica da Tabela Price.