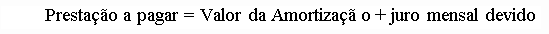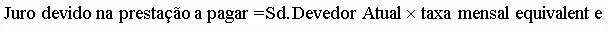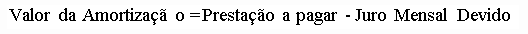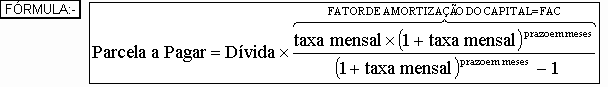O que está informado no artigo 1
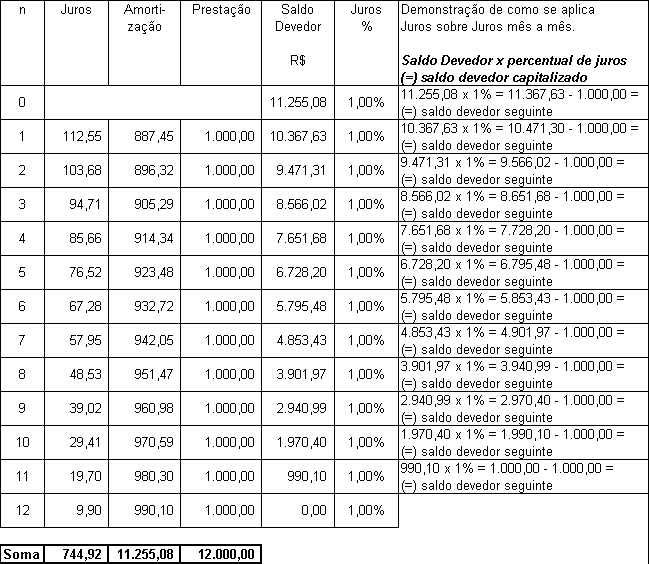
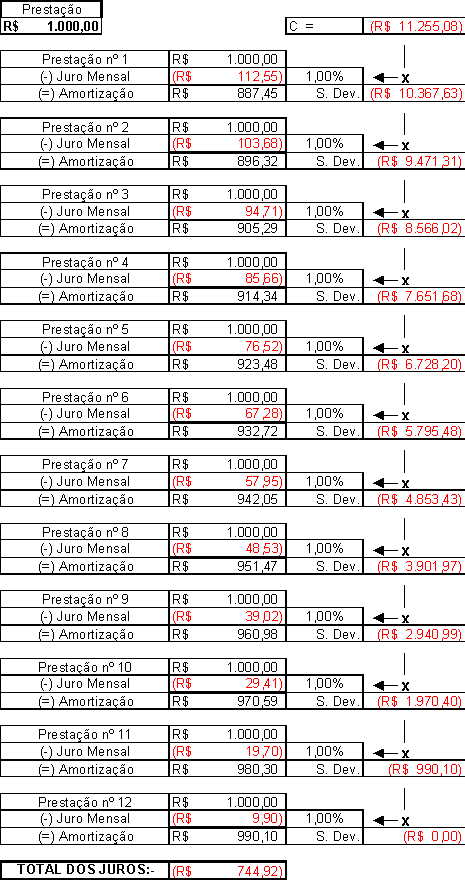
"Vamos aclarar a fórmula através de um exemplo que consistirá em calcular o financiamento de R$ 11.255,08, a ser pago em 12 (doze) parcelas mensais e consecutivas, com juros de 1% ao mês de acordo com a tabela price, cujo resultado são parcelas de R$ 1.000,00".
"Com efeito, na coluna da direita é possível visualizar perfeitamente os juros aplicados uns sobre os outros, vez que sempre incidentes sobre o novo valor de capital, antes da amortização".
O que realmente acontece
SISTEMA PRICE – CONCEITO: pagar, mensalmente, os juros sobre o saldo devedor e uma quota de amortização do capital.
O que está informado no artigo 2
"O problema fundamental da tabela price diz respeito à exigibilidade dos juros".
"Nesse sistema os juros tornam-se principal, enquanto o capital torna-se acessório. Isso porque os juros sobre todo o capital acumulado são recebidos primeiro, servindo o resíduo da prestação para amortizar o capital".
"O senso comum indica o contrário: os juros devem ser recebidos junto com a parcela de capital a que se referem, não antes, nem depois".
O que realmente acontece:
Em qualquer sistema de amortização, primeiro é pago OS JUROS SOBRE O SALDO DEVEDOR.
Os principais sistemas para fazer o resgate de um empréstimo, são:-
a) pagar, no vencimento, o capital e seus juros acumulados — SISTEMA DO MONTANTE (SM);
b) pagar, periodicamente, os juros sobre o capital e, no vencimento, o capital — SISTEMA AMERICANO (SAm);
c) pagar, periodicamente, os juros sobre o saldo devedor antecipadamente e uma quota de amortização do capital — SISTEMA ALEMÃO (SAI);
d) pagar, periodicamente, os juros sobre o saldo devedor e uma quota de amortização constante — SISTEMA HAMBURGUÊS ou SAC,
e) pagar, periodicamente, os juros sobre o saldo devedor e uma quota de amortização do capital — SISTEMA FRANCÊS (SF), e
e.1) pagar, mensalmente, os juros sobre o saldo devedor e uma quota de amortização do capital — SISTEMA PRICE.
O que está informado no artigo 3
"Antes de passar à proposta alternativa, examinemos alguns exemplos que demonstram a capitalização mensal de juros e a cobrança de juros sobre juros na tabela price":
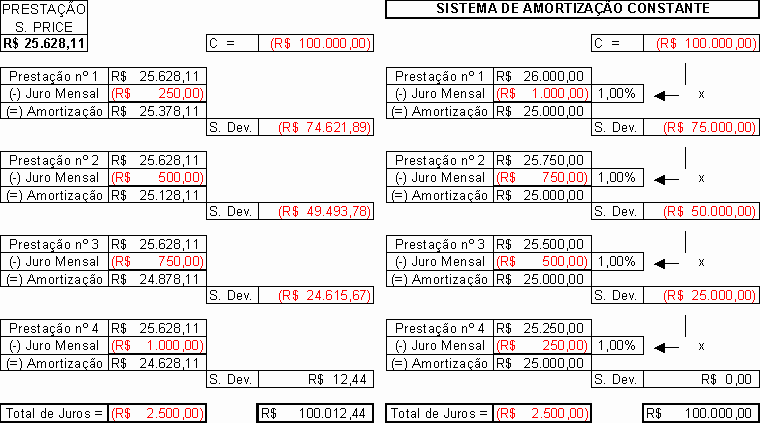
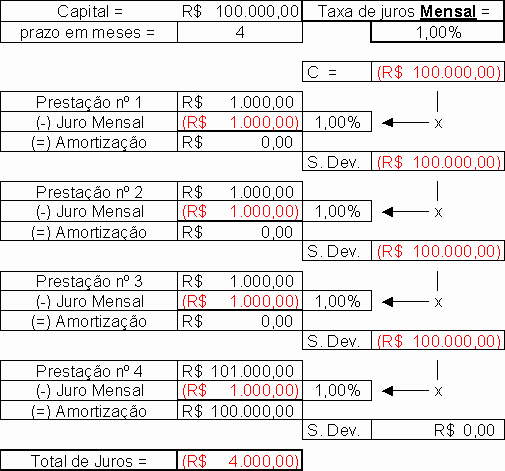
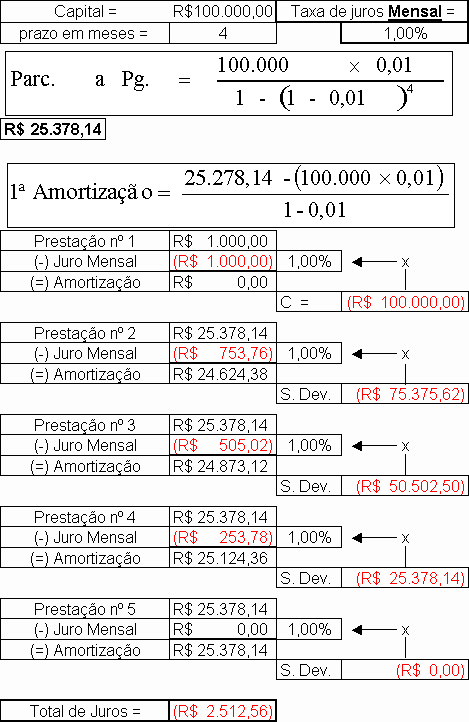
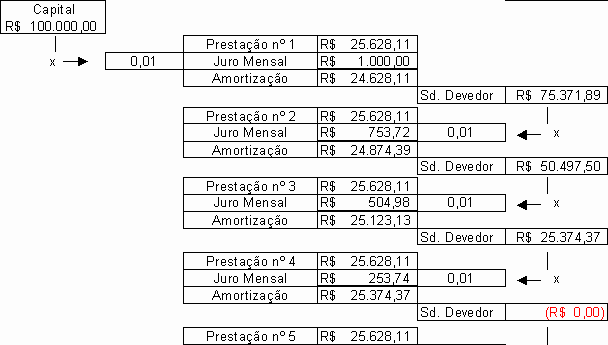
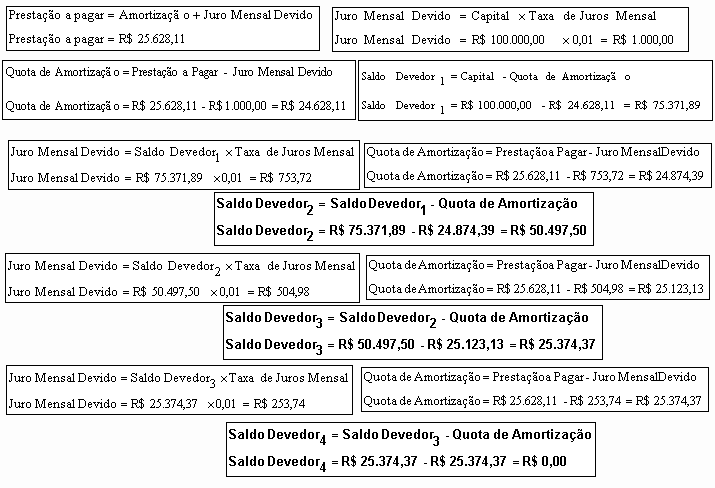
"Avaliemos, agora, o sistema de amortização pela tabela price para um financiamento de R$ 100.000,00 a ser pago em 4 parcelas mensais, com juros de 1% ao mês. Assim, o valor das prestações é calculado em R$ 25.628,11".
"Procedendo as amortizações como na tabela price , obviamente, chegará ao resultado que deseja, ou seja, que o saldo devedor seja R$ 0,09 (tendente a zero). É estarrecedor, mas alguns utilizam exatamente esse argumento para justificar que a tabela price não contém juros compostos!"
"Todavia, utilizado o sistema de juros simples, mantida a mesma parcela calculada pela tabela price , o resultado seria outro, a saber:"
"1a. parcela:
Saldo inicial: R$ 100.000,00 (somente capital);
Juros sobre a primeira fração de capital: R$ 250,00 (R$ 25.000,00 X 1% X 1 mês);
Parcela total (tabela price): R$ 25.628,11 (R$ 250,00 de juros e R$ 25.378,11 de amortização de capital);
Saldo no final do mês: R$ 74.621,89 devedor (R$ 100.000,00 – R$ 25.378,11).
2a. parcela:
Saldo anterior: R$ 74.621,89 (somente capital)
Juros sobre a segunda fração de capital: R$ 500,00 (R$ 25.000,00 X 1% X 2 meses);
Parcela total (tabela price): R$ 25.628,11 (R$ 500,00 de juros e R$ 25.128,11 de amortização de capital);
Saldo no final do mês: R$ 49.493,78 devedor (R$ 74.621,89 – R$ 25.128,11).
3a. parcela:
Saldo anterior: R$ 49.493,78 (somente capital)
Juros sobre a terceira fração de capital: R$ 750,00 (R$ 25.000,00 X 1% X 3 meses);
Parcela total (tabela price): R$ 25.628,11 (R$ 750,00 de juros e R$ 24.878,11 de amortização de capital);
Saldo no final do mês: R$ 24.615,67 devedor (R$ 49.493,78 – R$ 24.878,11).
4a. parcela:
Saldo anterior: R$ 24.615,67 (somente capital)
Juros sobre a quarta fração de capital: R$ 1.000,00 (R$ 25.000,00 X 1% X 4 meses);
Parcela total (tabela price): R$ 25.628,11 (R$ 1.000,00 de juros e R$ 24.628,11 de amortização de capital);
Saldo no final do mês: R$ 12,44 credor (R$ 24.615,67 – R$ 24.878,11)."
"Tendo sido cobrados juros de R$ 2.512,44 (R$ 25.628,11 X 4 – R$ 100.000,00), enquanto os devidos seriam R$ 2.500,00 (R$ 250,00 + R$ 500,00 + R$ 750,00 + R$ 1.000,00), chega-se à mesma conclusão que a memória de cálculo retro: o devedor teria saldo positivo de R$ 12,44, ou 0,4976% a mais em relação aos juros devidos".
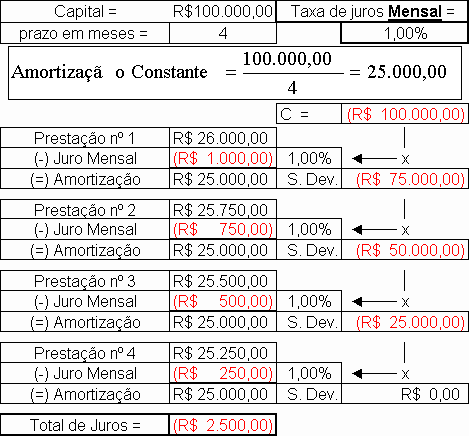
O método acima descrito, dito de sistema de juros simples, nada mais é do que o SISTEMA DE AMORTIZAÇÃO CONSTANTE ou HAMBURGUÊS, porém, com os juros invertidos, ou seja, os juros da última prestação paga-se na primeira, os juros da penúltima prestação paga-se na segunda, os juros da antipenúltima prestação paga-se na terceira prestação, etc., sendo utilizado como valor da prestação, a calculada pelo SISTEMA DE AMORTIZAÇÃO PRICE, ou seja, uma tremenda confusão, sem nenhuma base lógica.
Vejamos:
Ora, essa mistura do Sistema de Amortização Constante com juros mensais invertidos, e a prestação calculada pelo Sistema de Amortização Price, é um verdadeiro samba do crioulo doido.
Princípios sem fundamentos --pagar juros sobre fração do capital devolvido quando se deve outro valor-- levam a essas conclusões absurdas.
O que realmente acontece
SISTEMA DE AMORTIZAÇÃO PRICE
Como é que se pode utilizar o capital de R$ 100.000,00 por 1 mês e propor pagar juros somente sobre a quarta parte (R$ 25.000,00) do capital emprestado?
Como é que se pode utilizar o capital de R$ 74.621,89 por 1 mês e propor pagar juros somente sobre dois terço (R$ 50.000,00) do capital emprestado?
Como é que se pode utilizar o capital de R$ 49.493,78 por 1 mês e propor pagar juros sobre R$ 75.000,00?
Como é que se pode utilizar o capital de R$ 24.615,67 por 1 mês e propor pagar juros sobre R$ 100.000,00?
Que raciocínio brilhante!
desvirtua-se o conceito do Sistema de Amortização Price:- "pagar, mensalmente, os juros sobre o saldo devedor e uma quota de amortização do capital ";
cria-se um Sistema de Juros Simples, em que os juros são pagos em ordem inversa ao devido, ou seja, paga-se o juro mensal sobre o capital devolvido, e não sobre o saldo devedor, algo inédito na matemática financeira,
como num passe de mágica, após essa mistura fantástica, conclui que o exemplo demonstra "a capitalização mensal de juros e a cobrança de juros sobre juros na tabela price ".
O que está informado no artigo 4
"Não é incomum encontrarmos quem diga que primeiro se paga juros sobre todo o capital. Este argumento só se justifica se o contrato for mensal, ou seja, se for tomado um empréstimo hoje para devolução em 30 dias, quando serão pagos os juros totais e o capital integral".
"Não é o caso de empréstimos que duram 5, 10, 15 ou 20 anos, como os que normalmente são vinculados à aquisição da casa própria".
"Em suma, os argumentos normalmente apresentados não vislumbram outro sistema de amortização que não seja a tabela price (TP) para justificar-se. Em outras palavras, partem das conclusões da própria tabela price para validar os princípios da mesma e se valem dos princípios da tabela price para chegar às mesmas conclusões".
"São meros sofismas: se os princípios da tabela price forem considerados corretos, é evidente que suas conclusões também serão".
O que realmente acontece
Não existe nenhum sistema de amortização em que os juros não sejam cobrados sobre o saldo devedor, seja com prazo de 30 dias, 5, 10, 15 ou 20 anos.
Essa alegação é um absurdo. Os juros são sempre pagos sobre o valor que se deve (SALDO DEVEDOR), pelo simples fato de que tal valor não foi pago.
Vejamos os sistemas de amortizações mais utilizados no mundo:
SISTEMA DE AMORTIZAÇÃO CONSTANTE ou HAMBURGUÊS: pagar, periodicamente, uma quota de amortização constante e os juros sobre o saldo devedor
SISTEMA DE AMORTIZAÇÃO AMERICANO: pagar, periodicamente, os juros sobre o CAPITAL, e, no vencimento, o CAPITAL
SISTEMA DE AMORTIZAÇÃO ALEMÃO: pagar, periodicamente, juros ANTECIPADOS sobre o saldo devedor e uma quota de amortização do capital
SISTEMA DE AMORTIZAÇÃO PRICE: pagar, mensalmente, uma quota de amortização e os juros sobre o saldo devedor
Ao travar o conceito do sistema na questão da taxa de juros, SOMENTE SE A TAXA FOR ANUAL, e complementar que: COM PAGAMENTOS MENSAIS, surge a necessidade de se ter noção do que seja equivalência – se a taxa de juros é anual (exigência do sistema), qual seria sua equivalente mensal, já que os juros são pagos mensalmente?
Qual opção escolher?
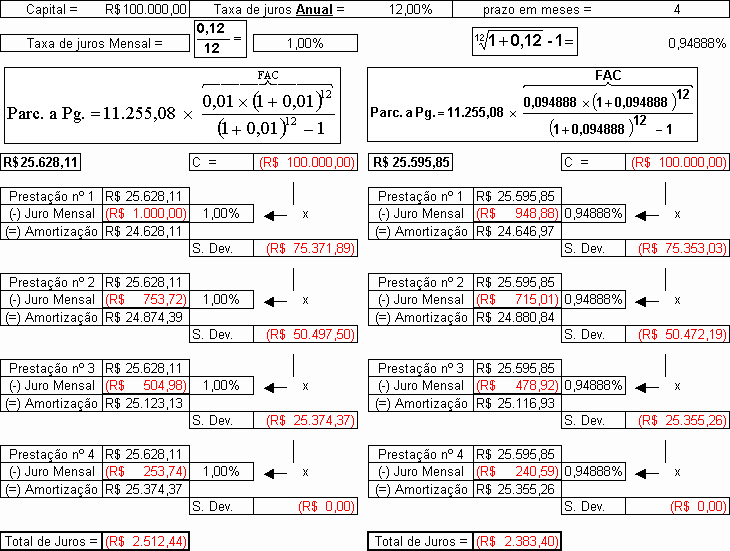
a)- pagar, durante 1 (um) ano, juros de 1% ao mês, ou
b)- pagar 12,68% ao ano de juros.
Qual opção escolher?
a)- pagar, durante 1 (um) ano, juros de 0,9489% ao mês, ou
b)- pagar 12% ao ano de juros.
É intrínseco do Sistema Price¾ que utiliza a soma de uma progressão geométrica, de razão 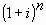
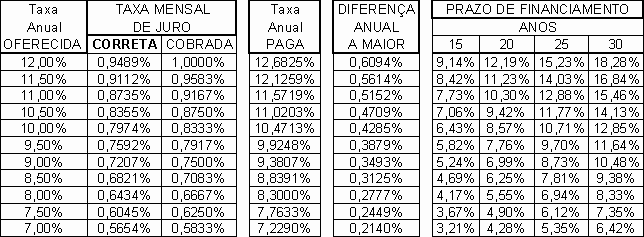
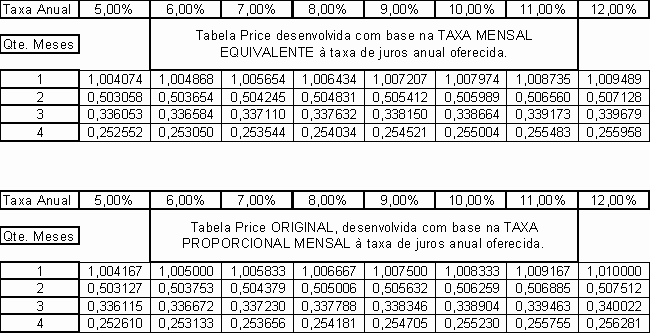
Acontece que a Tabela Price utiliza a divisão da taxa de juros anual por doze meses, ocasionando a cobrança de uma taxa anual maior do que a taxa oferecida.
A Tabela Price foi confeccionada dividindo a taxa anual oferecida por 12 meses, porém, quando é utilizado esse percentual mensal encontrado, na fórmula do Sistema Price, verifica-se que o percentual anual cobrado é maior do que a taxa inicialmente pactuada, por exemplo:- se taxa mensal for igual a 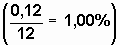
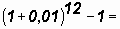
Portanto, quem utilizar os fatores de amortizações da Tabela Price, precisa entender que é inerente ao sistema esse aumento na taxa de juros anual.
Tem-se diferença paga a maior, devido ao aumento da taxa de juros anual oferecida:
Por exemplo, num financiamento de 25 anos a uma taxa anual oferecida de 7,00%, o mutuário pagaria 5,35% a maior, a título de juros.
Outro exemplo:- se o financiamento for de 30 anos a uma taxa de juros anual de 12,00%, o mutuário pagaria 18,28% a maior, a título de juros.
O que está informado no artigo 5
"Mesmo aqueles que conhecem o significado, dificilmente sabem demonstrar os labirínticos cálculos envolvidos e prever o alcance dos aumentos que serão carreados às parcelas em decorrência da aplicação da tabela price".
"Sendo assim, ainda que a tabela price não contivesse juros compostos, restaria inviável sua utilização no âmbito das relações de consumo em virtude do princípio da transparência esposado pelo Código de Defesa do Consumidor".
O que realmente acontece
Por exemplo:-
1)- Procura-se na Tabela Price original, o fator de amortização do capital (intersecção da linha de 4 meses com a coluna de 12% ao ano):- 0,256281.
2) Multiplique o fator de amortização do capital encontrado pelo valor do capital, e teremos o valor da prestação mensal devida:-
0,256281 x R$ 100.000,00 = 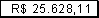
O único porém, ao se utilizar a Tabela Price original é que em vez de se pagar a taxa de juros oferecida de 12% ao ano, paga-se uma taxa anual maior: 12,68%.
Para corrigir essa distorção inerente ao Sistema Price, basta desenvolver a Tabela Price com base na taxa de juros mensal equivalente a taxa de juros anual oferecida.
Portanto, após o cálculo da prestação (Fator de Amortização do Capital fornecido pela Tabela Price multiplicado pelo Capital), basta fazer as operações matemáticas de multiplicar e diminuir para que se tenha toda a evolução do sistema de amortização.
Princípio da transparência para quem?
Multiplicar e dividir são operações que aprendemos nos primórdios de nossa formação escolar, e são consideradas informações básicas.
O Sistema de Amortização Price é perfeitamente legal e não pratica a cobrança de juros sobre juros.
A definição do Sistema de Amortização Price é simples:- paga-se, mensalmente, o juro mensal sobre o saldo devedor e uma quota de amortização .
A forma de amortização no Sistema Price é realizado da seguinte maneira:-
Em qualquer sistema de amortização, primeiro é pago O JURO SOBRE O SALDO DEVEDOR, seja ele, Americano, Hamburguês, Alemão, etc.
Outro aspecto inconfundível do Sistema de Amortização Price é:-
I – A TAXA DE JUROS TEM QUE SER, NECESSARIAMENTE, FIXADA EM TERMO ANUAL;
II – O PAGAMENTO DA PRESTAÇÃO TEM QUE SER, NECESSARIAMENTE, MENSAL.
Portanto, se a TAXA DE JUROS NÃO FOR FIXADA EM TERMO ANUAL, e os PAGAMENTOS NÃO FOREM MENSAIS, não a que se falar em SISTEMA PRICE.
O Sistema de amortização Price tem por finalidade fornecer o valor da prestação mensal , tendo como base:-
a)- Valor do Financiamento;
b)- prazo em meses para pagamentos, e
c)- taxa anual de juro pactuada.
O sistema se chama exatamente Price porque fornece uma fórmula em que é possível definir o percentual de juro anual que se deseja pactuar, porém, efetuando pagamentos mensais.
É o que tenho a comentar.
Notas
1 SCAVONE JÚNIOR, Luiz Antonio; GOMES, Pedro Afonso. A tabela Price é ilegal?. Jus Navigandi, Teresina, a. 5, n. 49, fev. 2001. Disponível em: <https://jus.com.br/artigos/736/a-tabela-price-e-ilegal>.
2 Idem.
3 Idem.
4 Idem.
5 Idem.