A capitalização composta de juros na tabela price ainda tem gerado muita polêmica. Há alguns anos escrevi alguns artigos nos quais tive como objetivo mostrar que no sistema francês de amortização - que no Brasil ficou conhecido como tabela price - de fato ocorre a capitalização composta dos juros.
Vários trabalhos foram criados no sentido de indicar qual o método que poderia trazer a eficiência econômica e técnica da TP, sem, contudo, promover a capitalização composta dos juros. Como alternativa de juros simples à tabela price, surgiram profissionais que passaram a defender a utilização do método de Gauss, o qual é perfeito para outras aplicações matemáticas/estatísticas, mas não serve como alternativa à tabela price.
Também começaram a surgir teses em defesa da utilização do SAC – sistema de amortização constante como alternativa de juros simples. Todavia, a exemplo do que acontece com a tabela price, o SAC somente aparenta ser desenvolvido sob o regime de capitalização simples, mas não é. No SAC também ocorre a capitalização composta de juros.
Pretendo, neste trabalho, provar e mostrar como ocorre a capitalização composta no SAC, fazendo uso das mesmas técnicas matemáticas que utilizei para provar que ocorre a capitalização composta na TP e também para evidenciar a ineficiência do método de Gauss como alternativa.
Em geral a decisão pela utilização de um sistema de amortização incorpora a ideia de planejamento e plenitude. Sua utilização permite saber quanto vai pagar, por quanto tempo, e que ao final do prazo estipulado a divida estaria sendo plenamente liquidada (pelo menos é isto que devia acontecer). Talvez a única exceção seja o Método Hamburguês, dadas suas particularidades.
Toda e qualquer operação que implique a aplicação de juros do tempo, representa uma espécie de fluxo de caixa, que, para os casos que se referem a dívidas contraídas, é tratada na literatura técnica especifica como Série de Pagamentos.
Há muito tempo tenho defendido que existe uma forma simples de verificar se, numa série de pagamentos, seja ela derivada ou não de um sistema de amortização, está havendo ou não a cobrança de juros compostos e/ou se ela atende aos requisitos de planejamento e plenitude acima referenciados. Pela aplicação dos conceitos matemáticos utilizados em análise de fluxos de caixa, isto se torna possível.
Para facilitar o entendimento do que se deseja mostrar, vamos daqui para frente seguir estudando alguns exemplos simples para, a partir deles, evoluirmos em nossa compreensão e aprendizado.
Primeiro vejamos um caso simples de empréstimo que foi combinado para ser pago em uma única prestação.
Exemplo 1
Empréstimo de R$ 100.000,00 a ser amortizado em uma única prestação ao final de 6 meses, com juros de 5% ao mês, calculados sob o regime de capitalização composta mensal. Qual o valor a ser pago ao final do prazo estipulado?

O objetivo aqui é o de apurar qual o valor da divida, calculada a juros compostos. Temos uma situação que representa uma serie de apenas 1 pagamento a ser realizado ao final do prazo estipulado, cujos juros serão calculados sob o regime de capitalização composta com periodicidade mensal. Neste caso basta aplicarmos a formula de juros compostos para saber qual o valor final a ser pago. Vejamos a seguir:
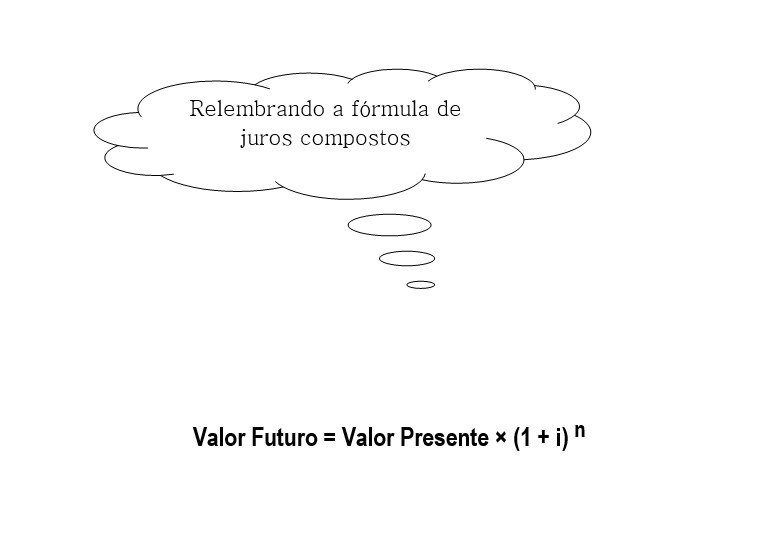
Aplicando a fórmula...
Valor Presente = Valor Futuro ÷ (1 + i)^n
Valor Futuro = 100.000,00 × (1,05)^6 = 134.009,56
Assim, o devedor deverá pagar como única prestação ao final de 6 meses o valor de R$ 134.009,56.
Mas, se tivéssemos a situação contrária, ou seja, temos o valor da divida e quiséssemos saber qual o valor emprestado?
Exemplo 2
Empréstimo que será pago em uma única parcela de R$ 134.009,56 ao final de 6 meses, com juros de 5% ao mês, calculados sob o regime de capitalização composta com periodicidade mensal. Qual o valor emprestado?

No exemplo acima temos o valor futuro (ou prestação) e queremos descobrir qual o valor da operação (capital ou valor presente).
Ajustando a fórmula, temos a seguinte situação:
Valor Presente = Valor Futuro ÷ (1 + i)^n
Valor Presente = 134.009,56 ÷ (1,05)^6 = 100.000,00
Aplicando a formula no sentido contrario (apuração do valor presente a partir do valor futuro) se obteve o valor original da operação.
Agora vamos supor uma situação em que quiséssemos saber o valor de uma dívida cujos juros foram calculados sob a forma de capitalização simples. Vejamos
Exemplo 3
Empréstimo de R$ 100.000,00 a ser amortizado em uma única prestação ao final de 6 meses, com juros de 5% ao mês, calculados sob o regime de capitalização simples mensal.


Aplicando a fórmula...
Valor Presente = Valor Futuro ÷ (1 + i × n)
Valor Futuro = 100.000,00 × (1 + 0,05 × 6) = 130.000,00
Se o juros fossem calculados sob o regime de capitalização simples o devedor estaria pagando uma única prestação de R$ 130.000,00 ao final dos 6 meses.
Vejamos agora como apurar o valor emprestado tendo o valor da dívida, que foi calculada a juros simples.
Exemplo 4
Empréstimo que será pago em uma única parcela de R$ 130.000,00 ao final de 6 meses, com juros de 5% ao mês, calculados sob o regime de capitalização simples. Qual o valor emprestado?
Ajustando a formula temos a seguinte situação:
Valor Presente = Valor Futuro ÷ (1 + i × n)
Valor Presente = 130.000,00 ÷ (1 +0,05 × 6) = 100.000,00
Aplicando a formula no sentido contrario (apuração do Valor Presente a partir do Valor Futuro) se obtem o valor original da operação.
Agora vamos propor uma situação completamente nova: sabemos qual o valor a ser emprestado, a taxa de juros, o prazo e o valor final da operação e queremos descobrir qual o regime de capitalização de juros aplicado.
Exemplo 5
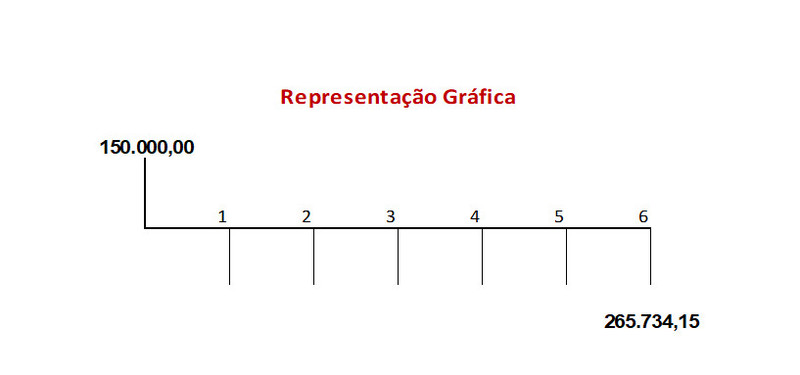
Empréstimo de R$ 150.000,00 pago em uma única prestação ao final de 6 meses, no valor de R$ 265.734,15. Sabendo que a taxa de juros mensal aplicada foi de 10% pergunta-se: qual o regime de capitalização de juros empregado?
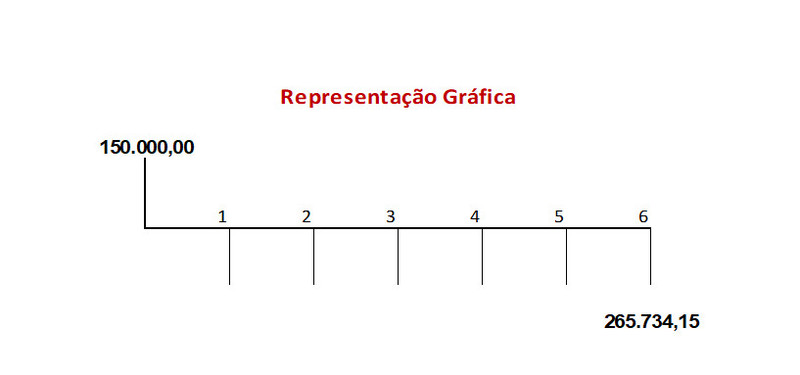
Como aconteceu nos exemplos anteriores, podemos fazer uso das fórmulas de juros simples ou compostos para saber qual o regime de capitalização fora empregado. Após aplicada a fórmula escolhida basta comparar o VP apurado com o valor indicado no problema. Vamos inicialmente aplicar a formula de juros simples.
Valor Presente = Valor Futuro ÷ (1 + i × n)
Valor Presente = 265.734,15 ÷ (1 + 0,10 × 6)
Valor Presente = 265.734,15 ÷ (1,60) = R$ 166.083,84
Como é possível ver o VP apurado (R$ 166.083,84) é diferente do valor indicado no problema (R$ 150.000,00). Sendo assim vamos aplicar a formula dos juros compostos para ver o que acontece
Valor Presente = Valor Futuro ÷ (1 + i)^n
Valor Presente = 265.734,15 ÷ 1,10^6
Valor Presente = 265.734,15 ÷ 1,771561
VP = R$ 150.000,00
Como é possível ver, o VP apurado (R$ 150.000,00) é igual ao valor indicado no problema (R$ 150.000,00). Neste passo é possível afirmar que na operação em debate houve o emprego do regime de capitalização composta de juros.
Se após a aplicação das fórmulas de juros simples e/ou compostos houvesse divergência entre os VP apurado e o indicado no problema, a hipótese mais plausível seria inconsistência de dados ou do modelo.
Daqui para frente, passaremos a ver operações com pagamento em várias prestações e mostraremos que a metodologia de Análise de Fluxo de Caixa também pode ser nelas utilizado, não importando o formato da Série de Pagamentos.
Para facilitar a compreensão, vamos desenvolver alguns exemplos usando o mesmo valor emprestado (R$ 100.000,00) e mesma taxa de juros (5% ao mês), variando apenas os formatos das séries de pagamentos e regime de capitalização dos juros.
Exemplo 6
Empréstimo que foi pago de acordo com a série de pagamentos indicada abaixo. Considerando que a taxa mensal de juros aplicada foi de 5% , sob o regime de capitalização composta mensal, pergunta-se: qual o valor emprestado?

No exemplo acima temos uma situação em que o empréstimo foi pago em prestações de valores aleatórios, mas definidas de tal forma que o empréstimo foi plenamente satisfeito.
Numa série de pagamentos cada prestação representa uma parte da operação. Assim para apurar qual o valor original da operação basta que apuremos e somemos o VP de cada prestação.
Ajustando a fórmula ao nosso exemplo, temos:
Valor Presentem =Valor Futurom ÷ (1 + i)^m
onde “m” representa o numero do termo
Vejamos o resultado da aplicação destes conceitos
VP 1 = |
20.000,00 |
÷ (1,05)^1 = |
R$ 19.047,62 |
VP 2 = |
10.000,00 |
÷ (1,05)^2 = |
R$ 9.070,29 |
VP 3 = |
5.000,00 |
÷ (1,05)^3 = |
R$ 4.319,19 |
VP 4 = |
22.250,00 |
÷ (1,05)^4 = |
R$ 18.305,13 |
VP 5 = |
30.000,00 |
÷ (1,05)^5 = |
R$ 23.505,78 |
VP 6 = |
34.510,12 |
÷ (1,05)^6 = |
R$ 25.751,98 |
Total |
R$ 100.000,00 |
Somando-se os VP mensais alcançamos o valor original da operação:
R$ 19.047,62 + (...) + R$ 25.751,98 = R$ 100.000,00
Para efeito didático elaboramos um quadro que mostra a evolução da operação:
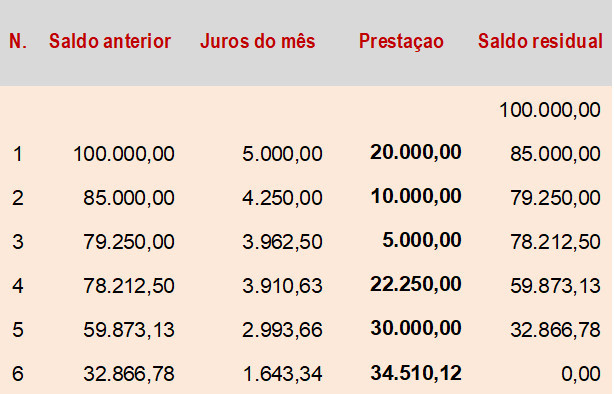
Como foi mostrado nos exemplos de uma única operação, se quiséssemos apenas verificar qual o regime de capitalização de juros empregado, bastaríamos utilizar as formulas de juros simples ou compostos em todas as prestações, apurar e somar os VPs mensais e comparar o valor apurado com o valor indicado no problema.
Por esta metodologia é possível saber, inclusive, quais as parcelas de capital e juros que cada prestação irá efetivamente amortizar.
Parcela de capital = VP mensal
Juros = Prestação – VP mensal
Da forma que as planilhas são normalmente apresentadas, o regime de capitalização fica um tanto quanto camuflado, o que, em minha opinião, tem sido o motivo de tanta polêmica. Somente pela decomposição detalhada da operação é possível “enxergar” a capitalização composta e ver, de fato, como ela se processa. Vejamos o quadro a seguir.
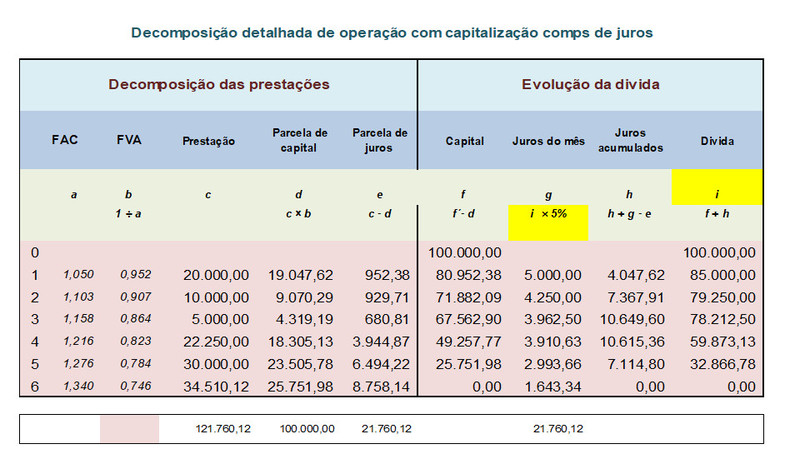
Passemos a explicar o quadro acima
1º mês: São apropriados juros de R$ 5.000,00 (coluna “g”) calculados sobre o saldo devedor (coluna “i”). Com o pagamento da prestação são amortizados R$ 19,047,62 (coluna “d”) de capital e R$ 952,38 de juros (coluna “e”) o saldo de juros não amortizados (R$ 4.047,62) passam a fazer parte da divida (coluna “h”) e também da base de calculo dos juros subsequentes (coluna “i)
-
2º mês: São apropriados juros de R$ 4.250,00 (coluna “g”), calculados sobre o saldo devedor (coluna “i”). Com o pagamento da prestação são amortizados R$ 9.070,29 (coluna “d”) de capital e R$ 929,71 de juros (coluna “e”) o saldo de juros não amortizados (R$ 7.367,91) passam a fazer parte da divida (coluna “h”) e também da base de calculo dos juros subsequentes (coluna “i”); e assim sucessivamente.
(...)
6º mês: São apropriados juros de R$ 1.643,34 (coluna “g”), calculados sobre o saldo devedor (coluna “i”). Com o pagamento da prestação são amortizados R$ 25.751.98 (coluna “d”) de capital e R$ 8.758,14 de juros (coluna “e”), e a divida é liquidada.
As técnicas de análise de Fluxo de Caixa podem ser aplicadas em qualquer formato de Série de Pagamentos. Vejamos mais alguns exemplos.
Exemplo 7
Empréstimo de R$ 100.000,00 que foi pago de acordo com a série de pagamentos indicada abaixo. Considerando que a taxa mensal de juros aplicada foi de 5%. Pede-se certificar se a serie de pagamentos foi calculada sob a forma de regime de capitalização composta.

Como visto, o objetivo do problema é mais especifico. Assim basta adaptarmos a metodologia à nossa necessidade. Vejamos.
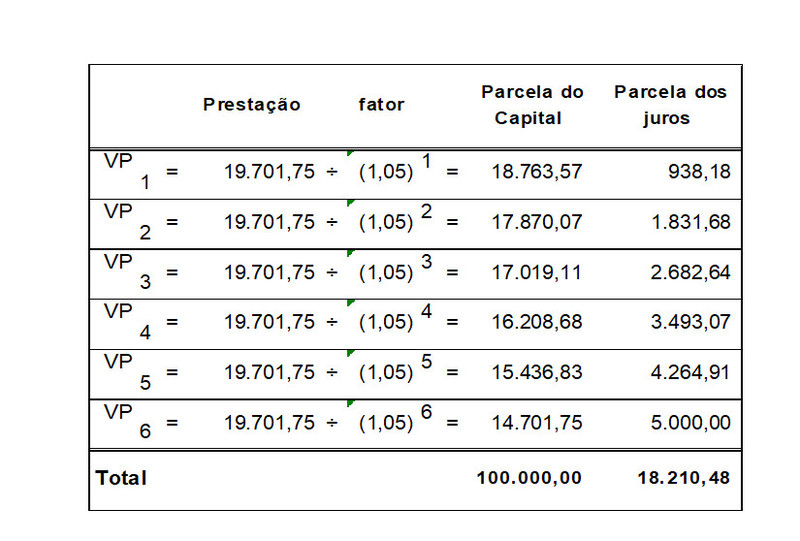
O quadro mostra que o valor da operação (somatório do VP das prestações) é igual ao valor indicado no problema. Também mostra quais as parcelas de capital e juros que cada prestação efetivamente amortiza. Façamos agora a decomposição detalhada da operação:
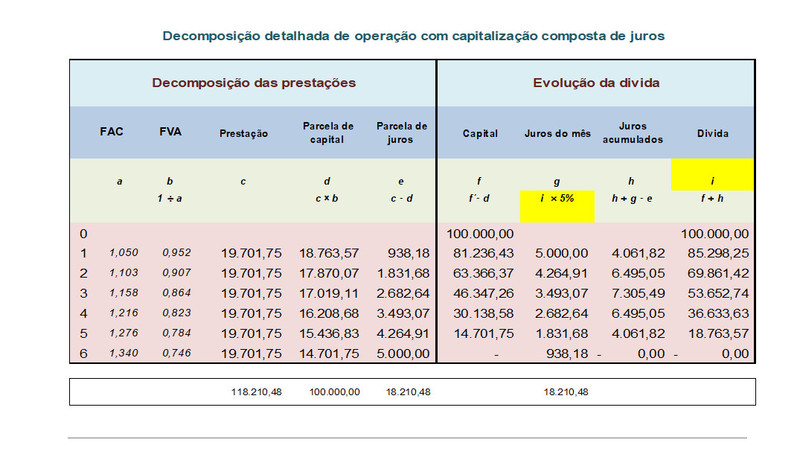
Detalhando...
1º mês: São apropriados juros de R$ 5.000,00 (coluna “g”). Com o pagamento da prestação são amortizados R$ 18.763,57 (coluna “d”) de capital e R$ 938,18 de juros (coluna “e”). O saldo de juros não amortizados (R$ 4.061,82 – coluna “h”) passam a fazer parte da divida e também da base de calculo dos juros subsequentes (coluna “i”);
2º mês: São apropriados juros de R$ 4.264,91 (coluna “g”), calculados sobre o saldo devedor (coluna “i|). Com o pagamento da prestação são amortizados R$ 17.870,07 de capital (coluna “d”) e R$ 1.831,68 de juros (coluna “d”). O saldo de juros não amortizados (R$ 6.495,05 – coluna “h”) passam a fazer parte da divida (coluna “f”) e também da base de calculo dos juros subsequentes;
(...)
6º mês: São apropriados juros de R$ 938,18 (coluna “g”), calculados sobre o saldo devedor (coluna “i”). Com o pagamento da prestação são amortizados R$ 14.701,75 (coluna “d”) de capital e R$ 5.000,00 de juros (coluna “e”); o saldo de capital e juros são liquidados.
Vamos a outro exemplo.
Exemplo 8
Empréstimo de R$ 100.000,00 e foi pago de acordo com a série de pagamentos indicada abaixo. Considerando que a taxa mensal de juros aplicada foi de 5%, pede-se certificar se a serie de pagamentos foi calculada sob a forma de regime de capitalização composta.

Aplicando as técnicas de análise de Fluxo de Caixa temos a seguinte situação:
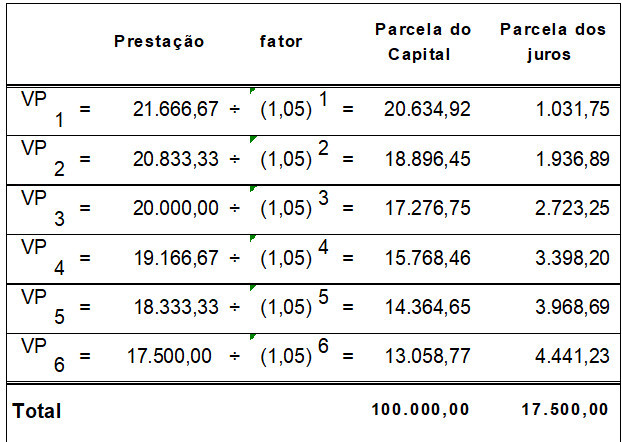
Pela decomposição das parcelas vimos que o valor apurado é igual ao valor indicado no problema. Assim, é possível afirmar que a Série de Pagamentos foi montada sob o regime de juros compostos. Para efeito didático vejamos como a operação seria normalmente apresentada:
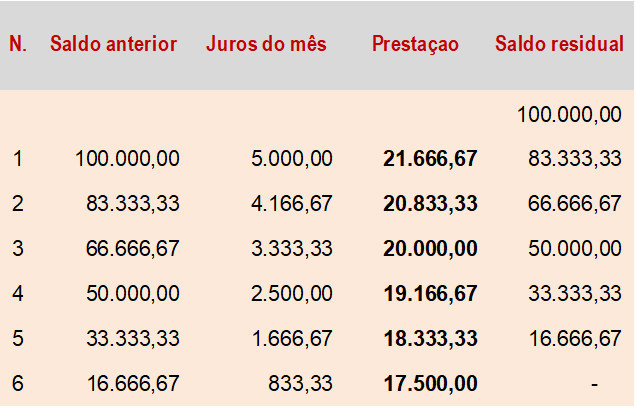
Como visto, a capitalização composta ficou “mascarada”. Vamos a decomposição detalhada da operação:
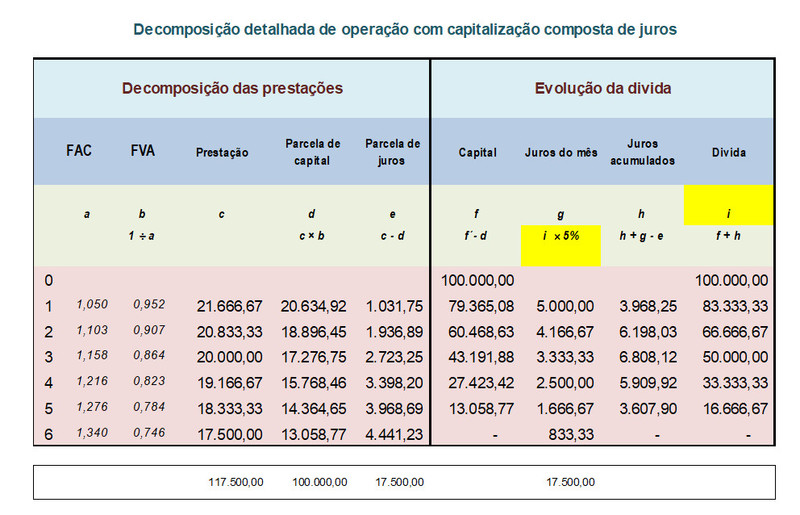
A operação acima foi desenvolvida pelo SAC- Sistema de Amortização Constante.
A grande questão é que surgiram algumas teses que passaram a apresentar o SAC como alternativa de juros simples. Todavia, como mostrado, no SAC os juros são cobrados sob o regime de capitalização composta de juros
Sendo assim, a exemplo do que também já explorei em trabalhos anteriores, pela manipulação adequada da metodologia aplicada a análise de fluxos de caixa é possível criar métodos alternativos, sob o regime de capitalização simples.
Sistema de Prestações Iguais a juros simples
Como não é possível deduzir uma única formula, é necessário que lancemos mão de uma planilha para realizar os cálculos. Pelo método que será proposto é possível deduzir uma prestação que proporcione a amortização do empréstimo no tempo programado sem que haja a incidência de juros sobre juros (juros compostos)
Exemplo 9
Empréstimo de R$ 100.000,00 a ser pago em seis prestações mensais e iguais a taxa de 5% mês, sob o regime da capitalização simples de juros. Pede-se calcular qual o valor da prestação.
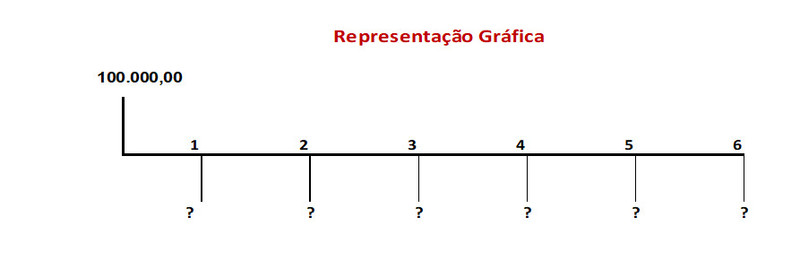
Procedimentos a serem adotados
1º passo: Apurar o FACmensal - Fator de Acumulação de Capital mensal, da seguinte forma
FAC mês = (1 + i × n)
2º passo: Apurar o FVA mês – Fator de Valor Atual mensal:
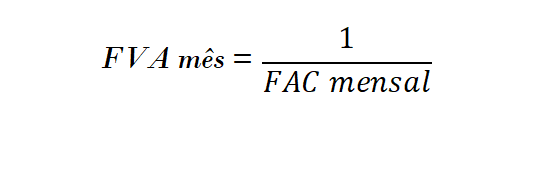
3º passo: Apurar o FRC – Fator de Recuperação do Capital:
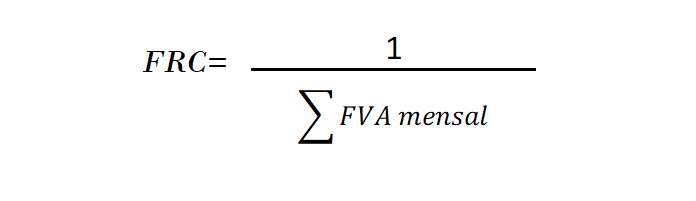
4º passo: Apurar o valor da prestação:
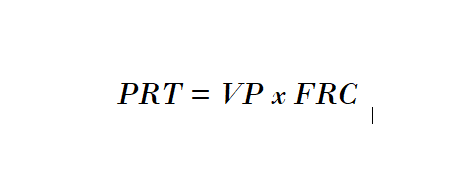
Vamos aplicar a metodologia no exemplo acima:
FVA1 = 1 ÷ ( 1 + 0,05 × 1) = 0,9524
FVA2 = 1 ÷ ( 1 + 0,05 × 2) = 0,9091
FVA3 = 1 ÷ ( 1 + 0,05 × 3) = 0,8696
FVA4 = 1 ÷ ( 1 + 0,05 × 4) = 0,8333
FVA5 = 1 ÷ ( 1 + 0,05 × 5) = 0,8000
FVA6= 1 ÷ ( 1 + 0,05 × 6) = 0,7692
∑ FVA mensal = 5,133601
FRC = 1 ÷ 5,133601 = 0,194795
PRT = 100.000,00 x 0,19795
Prestação = 19.479,50
Pela aplicação da metodologia acima, o valor da prestação para atender as condições estabelecidas é de R$ 19.479,50. Para efeito de certificação, vamos decompor as prestações e a dívida para confirmar se o valor está correto.
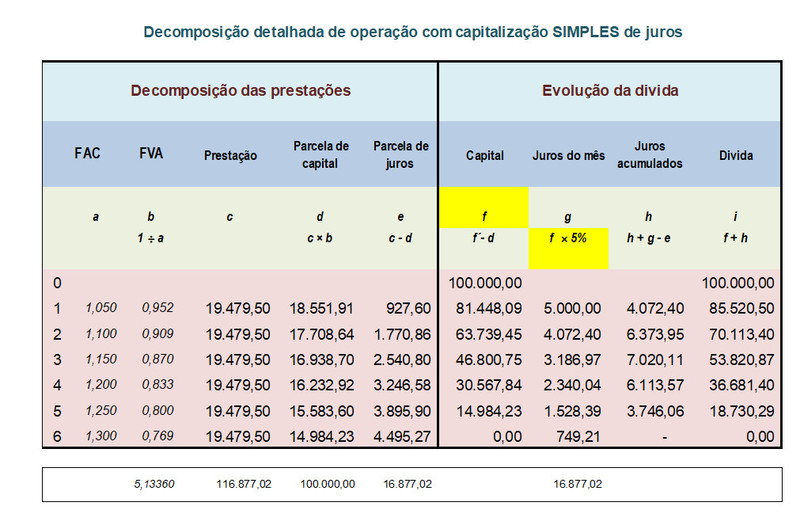
Explicação pormenorizada do quadro:
1º mês: São apropriados juros de R$ 5.000,00 (coluna “g”) calculados apenas sobre o capital. Com o pagamento da prestação são amortizados R$ 18.551,91 (coluna “d”) de capital e R$ 927,60 de juros (coluna “e”). O saldo de juros não amortizados (R$ 4.072,40) passa a fazer parte da divida (coluna “i”), mas não da base de calculo dos juros subsequentes;
-
2º mês: São apropriados juros de R$ 4.072,50 (coluna “g”) calculados apenas sobre o capital. Com o pagamento da prestação são amortizados R$ 17.708,64 (coluna “d”) de capital e R$ 1.770.86 de juros (coluna “e”). O saldo de juros não amortizados (R$ 6.373,95) passa a fazer parte da divida (coluna “i”), mas não da base de calculo dos juros subsequentes;
3º mês: São apropriados juros de R$ 3.186,97 (coluna “g”) calculados apenas sobre o capital. Com o pagamento da prestação são amortizados R$ 16.938,70 (coluna “d”) de capital e R$ 2.540,80 de juros (coluna “e”). O saldo de juros não amortizados (R$ 7.020,11) passa a fazer parte da divida (coluna “i”), mas não da base de calculo dos juros subsequentes;
(...)
6º mês: São apropriados juros de R$ 749,21 (coluna “g”) calculados apenas sobre o capital. Com o pagamento da prestação são amortizados R$ 14.984,23 de capital e R$ 4.495,27 de juros e a divida é plenamente liquidada.
Embora não pareça, foi a partir desta metodologia que a fórmula da TP foi criada. Apenas para efeito de constatação da consistência técnica vamos usar esta mesma metodologia para apurar a prestação para o regime de juros compostos.
FVA1 = 1 ÷ (1 + 0,05) 1 = 0,952
FVA2 = 1 ÷ (1 + 0,05) 2 = 0,907
FVA3 = 1 ÷ (1 + 0,05) 3 = 0,864
FVA4 = 1 ÷ (1 + 0,05) 4 = 0,823
FVA5 = 1 ÷ (1 + 0,05) 5 = 0,784
FVA6 = 1 ÷ (1 + 0,05) 6 = 0,746
∑ FVA mensal = 5,07569
FRC = 1 ÷ 5,07569 = 0,197017
PRT = 100.000,00 x 0,197017
Prestação = 19.701,75
Pela aplicação desta metodologia, apuramos que o valor da prestação para o regime de capitalização composta é de R$ 19.701,75, que é o mesmo valor indicado no problema exposto no exemplo 7, no qual havíamos utilizado a tabela price como sistema de amortização.
Considerações Finais
Todos os sistemas de amortização aplicados nas principais operações de credito compreendem o regime de capitalização composta de juros, dentre os quais se destacam a SFA – TP e o SAC.
Como explorado em outro trabalho, o método de Gauss fora inicialmente apresentado como alternativa de juros simples à tabela price. Todavia, embora seja perfeito para os objetivos para os quais ele foi criado, não serve como alternativa, porque ele resulta numa prestação de valor menor à ideal.
Como mostrado, pela manipulação adequada das técnicas aplicadas à análise de fluxo de caixa, é possível certificar a consistência da série de pagamentos criada, verificar qual o regime de capitalização empregado e/ou desenvolver modelos que permitem criar séries de pagamentos que possibilitem liquidar operações, sem que ocorra a incidência de juros sobre juros (capitalização composta).




