Vários dos sistemas de amortização utilizados e/ou conhecidos no Brasil incorporam a teoria de juros compostos. Um deles, e talvez o mais popular, é o Sistema Francês de Amortização, que no Brasil é conhecido como Tabela Price. Ele é muito utilizado em contratos de financiamento imobiliário e operações de Crédito Direto ao Consumidor.
Depois de muita discussão em torno deste tema, surgiram alguns trabalhos e decisões nos tribunais a favor da utilização do Método de Gauss. Todavia referido sistema não serve como alternativa de juros à TP.
Escrevi alguns artigos que tratam da Tabela Price. No primeiro, em 2000, mostrei de forma muito singela um método que elaborei que serve como alternativa de juros simples. No último demonstrei porque o Método de Gauss não serve como alternativa.
O objetivo deste trabalho é falar um pouco da Tabela Price, tratar novamente (e mais profundamente) do método que elaborei e, por fim, falar do Método de Gauss.
Vamos fazer uso de alguns exemplos e evoluir em nossa compreensão.
Exemplo 1
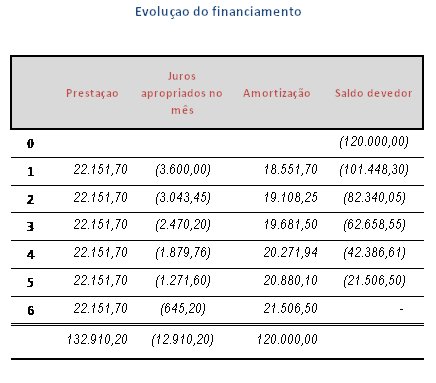
Sabendo-se que a venda de um determinado imóvel no valor de R$ 120.000,00 foi realizada mediante o pagamento de 6 prestações mensais, iguais e sucessivas a juros compostos de 3% ao mês pergunta-se: qual o valor de cada prestação?
Aplicando a fórmula da TP temos:
Prestação =120.000 x __(1,03)^6 x 0,03___ = 22.151,70
(1,03)^6 -1
Vejamos como ficaria a evolução do financiamento pela forma que normalmente seria demonstrado:
Todavia, para atender ao objetivo do nosso estudo vamos apurar o fator de cálculo da prestação (FRC) e o valor da prestação, a partir do modelo matemático com base no qual a formula da TP foi criada.
Relembrando a fórmula de juros compostos ...
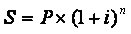 |
=> |
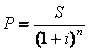 |
=> |
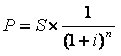 |
onde ...
(1 + i)^n = Fator de Acumulação de Capital – FAC
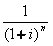 |
=> Fator de Valor Atual - FVA |
Para obter o valor original da operação teríamos que realizar as seguintes operações:
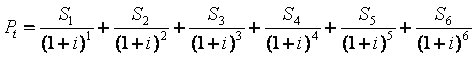
S1 + S2 + S3 + S4 + S5 + S6 =R
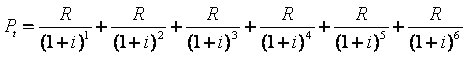
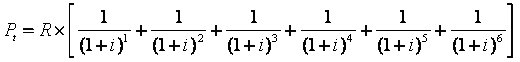
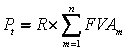
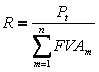
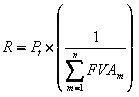
onde |
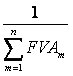 |
representa o fator de calculo da prestação (FRC – Fator de Recuperação da Operação) |
Aplicando o modelo ao exemplo citado, temos:
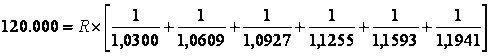
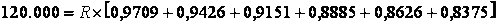
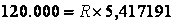
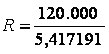
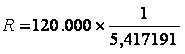
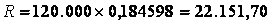
Para facilitar os cálculos vamos apurar o FRC com o auxilio de uma planilha eletrônica.
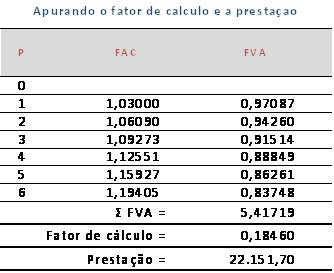
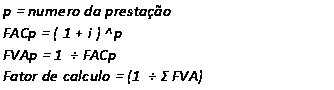
Nosso exemplo representa um fluxo de caixa onde cada prestação representa o montante (ou valor futuro) de um capital individual que desconhecemos aplicado à taxa de 3% ao mês, a juros compostos, em prazos que variam de 1 a 6 meses. Neste caso conhecemos os valores futuros destas operações e através da decomposição das prestações será possível descobrir quais os valores de capital e de juros individuais.

Para sabermos os Valores Atuais desta Serie de Pagamentos e, consequentemente, o Valor Atual total da operação basta fazermos a decomposição das prestações.
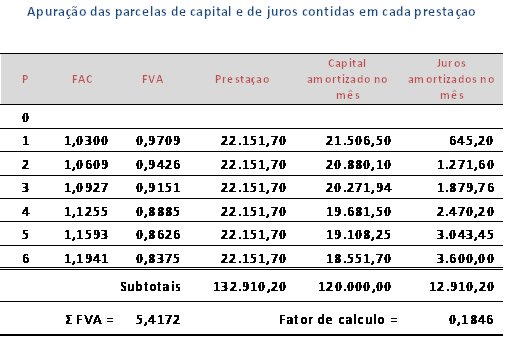

Fazendo a decomposição dos saldos de capital e dos juros é possível enxergar a capitalização composta dos juros:
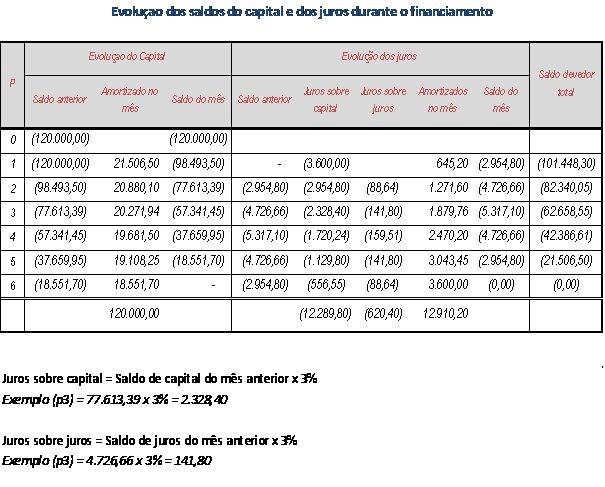
Para quem está concedendo, o empréstimo só valerá a pena se ela estiver lhe proporcionando o mesmo retorno financeiro que obteria se aplicasse o capital “investido” `a mesmas condições financeiras (taxa de juros, prazo e regime de capitalização).
Valor Futuro = Valor Presente x (1 + i )^n
Valor Futuro = 120.000,00 x 1,03^6 = 143.286,28
Fazendo-se a evolução das prestações temos a seguinte situação:
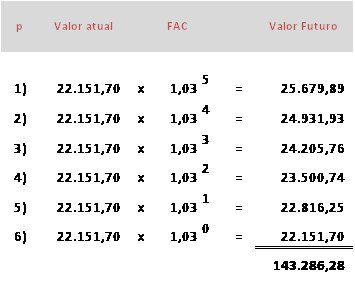
Cada uma das prestações comporta uma parcela de capital e outra de juros. A aplicação dos fatores indicados para cada mês estaria ocasionando a apropriação de juros sobre juros (juros do período que vai desde o pagamento da prestação até o final do período de apuração que está sendo apropriado sobre os juros contidos em cada prestação) Como o sistema é desenvolvido com juros compostos este procedimento não causa nenhuma distorção.
Mas existe outra forma de fazermos estes cálculos que vai gerar o mesmo resultado e será muito útil ao objetivo do nosso estudo. Basta fazermos a evolução tomando por base os Valores Atuais de cada prestação. Vejamos a seguir:
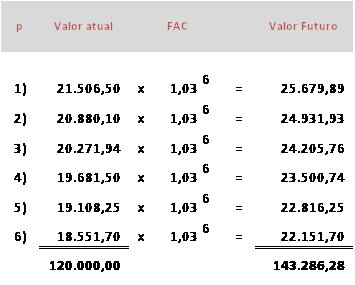
Os Valores Atuais de cada prestação representam as parcelas de capital no momento em que a operação foi celebrada; por esta razão todos eles devem ser capitalizados pelos 6 meses. O motivo para utilizar este método ficará mais claro à frente, quando estudarmos o sistema de juros simples e falarmos novamente sobre o Método de Gauss.
Quero aproveitar também para falar um pouco mais sobre a forma de pagamento (amortização) dos juros mensais. Muitos colegas ainda compartilham a ideia de que com o pagamento da prestação os juros apropriados no mês são totalmente quitados, razão pela qual não ocorre a capitalização composta dos juros (não existirão juros a sofrerem juros do período subsequente). Isto não é verdade. Cada uma das prestações amortiza apenas uma parte dos juros devedores. Se a operação foi elaborada a juros compostos, os saldos mensais dos juros, não quitados pela prestação, serão incorporados à base de calculo dos juros do mês subsequente. Se a operação foi elaborada a juros simples os juros não liquidados pela prestação não serão incorporados à base de cálculo dos juros do mês subsequente. Na nossa planilha a coluna “juros sobre juros” representa o resultado da capitalização composta.
Vamos examinar cada uma das prestações para ver como isto funciona
1ª prestação: com o pagamento desta prestação o mutuário está amortizando R$ 21.506,50 de capital e R$ 645,20 de juros. No primeiro mês foram apropriados R$ 3.600,00. Com o pagamento da prestação restaram R$ 2.954,80 de juros que não foram pagos (R$ 3.600,00 – R$ 645,20) e que serão incorporados a base de cálculo do mês subsequente.
2ª prestação: com o pagamento desta prestação o mutuário estará amortizando R$ 20.880,10 de capital e R$ 1.271,60 de juros. No mês foram apropriados R$ 3.043,05 (R$ 2.954,80 de juros sobre capital + R$ `88,64 de juros sobre juros) que somados ao saldo anterior de R$ 2.954,80 acumulam R$ 5.998,25. Deste valor restaram R$ 4.726,66 (R$ 5.998,25 – R$ 1.271,60) que incorporarão a base de cálculo dos juros do mês subsequente.
3ª prestação: com o pagamento desta prestação o mutuário estará amortizando R$ 20.271,94 de capital e R$ 1.879,76. No mês foram apropriados R$ 2.470,20 (R$ 2.328,40 de juros sobre capital + R$ 141,80 de juros sobre juros) que somados ao saldo anterior de R$ 4.726,66 acumulam R$ 7.196,86. Deste valor restarão R$ 5.317,10 (R$ 7.196,86 – R$ 1.879,76) que incorporarão a base de cálculo dos juros do mês subsequente.
4ª prestação: com o pagamento desta prestação o mutuário estará amortizando R$ 19.681,50 de capital e R$ 2.470,20. No mês foram apropriados R$ 1.879,76 (R$ 1.720,24 de juros sobre capital + R$ 159,51 de juros sobre juros) que somados ao saldo anterior de R$ 5.317,10 acumulam R$ 7.196,86. Deste valor restarão R$ 4.726,66 (R$ 7.196.86 – R$ 2.470,20) que incorporarão a base de cálculo dos juros do mês subsequente.
5ª prestação: com o pagamento desta prestação o mutuário estará amortizando R$ 19.108,25 de capital e R$ 3.043,05. No mês foram apropriados juros de R$ 1.271,60 (R$ 1.129,80 de juros sobre capital + R$ 141,80 de juros sobre juros) que somados ao saldo anterior de R$ 4.726,66 acumulam R$ 5.998,25. Deste valor restarão R$ 2.954,80 (R$ 5.998,25 – R$ 3.043,45) que incorporarão a base de cálculo dos juros do mês subsequente.
6ª prestação: com o pagamento desta prestação o mutuário estará amortizando R$ 18.551,70 de capital e R$ 3.600,00. No mês foram apropriados juros de R$ 645,20 (R$ 556,55 de juros sobre capital + R$ 88,64 de juros sobre juros) que somados ao saldo anterior de R$ 2.954,80 acumulam R$ 3.600,00. Este valor será liquidado com o pagamento da prestação (R$ 3.600,00 – R$ 3.600,00)..
O desafio aqui é o de encontrar um modelo matemático que sirva como alternativa de juros simples. Vamos então adaptar os exemplos à nossa necessidade.
Exemplo 2
A venda de um determinado imóvel no valor de R$ 120.000,00 foi financiada em 6 prestações mensais, iguais e sucessivas com sistema de capitalização simples de juros. Sabendo-se que a taxa de juros é de 3% qual o valor de cada prestação?
Não existe, ainda, uma fórmula que mostre qual o valor ideal de prestação para atender a esta situação. Por esta razão é que temos que apurar o fator de cálculo (FRC) e o valor da prestação aplicando o mesmo raciocínio indicado acima. Vamos a ele.
Relembrando as fórmulas de juros simples...
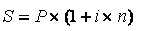 |
=> |
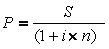 |
=> |
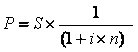 |
onde ...
(1 + i x n) => Fator de Acumulação de Capital – FAC
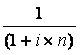 |
=> Fator de Valor Atual - FVA |
Assim, adaptando o modelo utilizado no Exemplo 1 temos a seguinte situação:
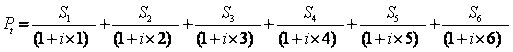
S1 + S2 + S3 + S4 + S5 + S6 =R
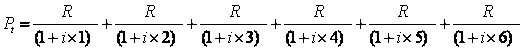
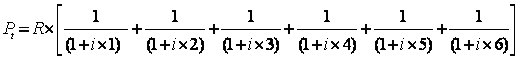
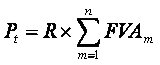
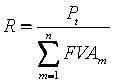
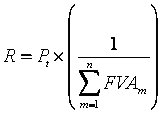
onde |
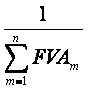 |
representa o fator de calculo da prestação (FRC) |
Aplicando o modelo ao nosso caso...
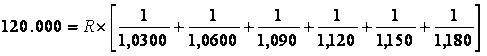
120.000 = R×[0,97087+0,94340+0,91743+0,89286+0,86957+0,84746]
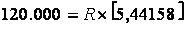
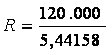
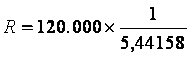
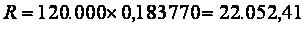
Vejamos como fica a apuração do fator de cálculo (FRC) e da prestação com o auxilio de uma planilha eletrônica.
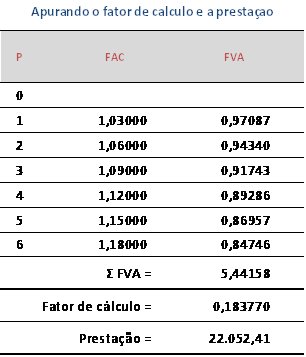

Agora vamos fazer a decomposição das prestações para descobrir quais as parcelas de capital e de juros que cada uma estará efetivamente amortizando.

Falta ainda mostrar como fica a evolução dos saldos de capital e dos juros.
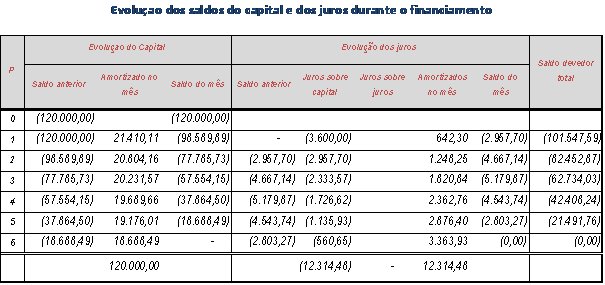
Vale observar a coluna “Juros sobre juros” que não tem nenhum valor apropriado. Vamos examinar cada uma das prestações para explicar isto melhor.
1ª prestação: com o pagamento desta prestação o mutuário está amortizando R$ 21.410,11 de capital e R$ 642,30 de juros. No primeiro mês foram apropriados R$ 3.600,00. Com o pagamento da prestação restaram R$ 2.957,70 de juros que não foram pagos (R$ 3.600,00 – R$ 642,30) que não serão incorporados à base de cálculo do mês subsequente, ou seja, no mês seguinte os juros serão apropriados somente sobre o saldo do capital.
2ª prestação: com o pagamento desta prestação o mutuário estará amortizando R$ 20.804,16 de capital e R$ 1.248,25 de juros. No mês foram apropriados R$ 2.957,70 (juros somente sobre capital) que somados ao saldo anterior de R$ 2.957,70 acumulam R$ 5.915,39. Deste valor restou R$ 4.667,15 (R$ 5.915,39 – R$ 1.248,25) que não serão incorporados à base de cálculo dos juros do mês subsequente, ou seja, no mês seguinte os juros serão apropriados somente sobre o saldo do capital.
-
3ª prestação: com o pagamento desta prestação o mutuário estará amortizando R$ 20.231,57 de capital e R$ 1.820,84 de juros. No mês foram apropriados R$ 2.333,57 (juros somente sobre capital) que somados ao saldo anterior de R$ 4.667,14 acumulam R$ 7.000,72. Deste valor restou R$ 5.179,87 (R$ 7.000,72 – R$ 1.820,84) que não serão incorporados à base de cálculo dos juros do mês subsequente, ou seja, no mês seguinte os juros serão apropriados somente sobre o saldo do capital.
4ª prestação: com o pagamento desta prestação o mutuário estará amortizando R$ 19.689,66 de capital e R$ 2.362,76 de juros. No mês foram apropriados R$ 1.726,62 (juros somente sobre capital) que somados ao saldo anterior de R$ 5.179,87 acumulam R$ 6.906,50. Deste valor restou R$ 4.543,74 (R$ 6.906,50 – R$ 2.362,76) que não serão incorporados à base de cálculo dos juros do mês subsequente, ou seja, no mês seguinte os juros serão apropriados somente sobre o saldo do capital.
5ª prestação: com o pagamento desta prestação o mutuário estará amortizando R$ 19.176,01 de capital e R$ 2.876,40 de juros. No mês foram apropriados R$ 1.135,93 (juros somente sobre capital) que somados ao saldo anterior de R$ 4.543,74 acumulam R$ 5.679,67. Deste valor restou R$ 2.803,27 (R$ 5.679,67 – R$ 2.876,40) que não serão incorporados à base de cálculo dos juros do mês subsequente, ou seja, no mês seguinte os juros serão apropriados somente sobre o saldo do capital.
6ª prestação: com o pagamento desta prestação o mutuário estará amortizando R$ 18.688,49 de capital e R$ 3.363,93 de juros. No mês foram apropriados R$ 560,65 (juros somente sobre capital) que somados ao saldo anterior de R$ 2.803,27 acumulam R$ 3.363,93. Este valor será liquidado com o pagamento da prestação (R$ 3.363,93 – R$ 3.363,93).
Como ficaria esta operação do ponto de vista do investidor.
Valor Futuro = Capital × (1 + i × n)
Valor Futuro = 120.000,00 × (1 + 0,03 × 6) = 141.600,00
Cada uma das prestações é composta de parcelas de capital e juros. Considerando que o modelo foi desenvolvido com juros simples não podemos iniciar a série com o valor das prestações, porque estaríamos aplicando juros sobre juros. Temos que fazer a evolução tomando por base os Valores Atuais de cada prestação.
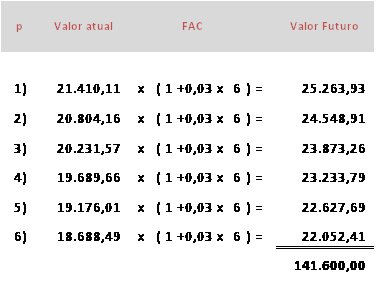
Somente para ilustrar vejamos qual a distorção que ocorreria se fizéssemos este mesmo cálculo partindo de cada prestação:
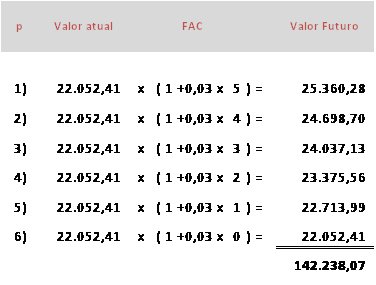
Os Fatores de Acumulação de Capital – FAC desta série foram calculados sob a forma de capitalização simples. A aplicação deles, por si só, não causaria nenhuma distorção não fosse o fato de que nas prestações existem parcelas de juros. Aplicando o raciocínio acima estar-se-ia promovendo a apropriação de juros (representados pelos fatores) sobre os juros contidos em cada prestação.
É exatamente por esta razão que o Método de Gauss não serve como alternativa. Ele se baseia na Soma de Termos de uma Progressão Aritmética. Partindo de um determinado valor (neste caso, R$ 141.600,00) ele permite calcular o valor do termo (prestação) cuja soma de uma determinada progressão aritmética aplicada sobre ele, resulte no valor esperado. Vejamos o que acontece se fizermos a amortização pelo Método de Gauss.
Relembrando a fórmula...
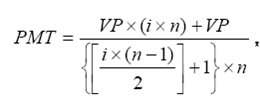
Aplicando a formula acima ao nosso exemplo apuraríamos que o valor da prestação alcança o valor de R$ 21.953,49. Já sabemos que se aplicado a juros simples de 3% ao mês, durante os 6 meses, o investidor obteria o montante de R$ 141.600,00. Assim para decidir pelo empréstimo o investidor deverá obter o mesmo retorno. Fazendo os cálculos a partir das prestações temos o seguinte:
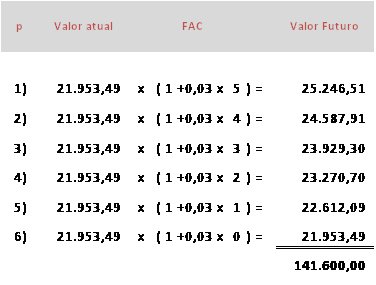
A aplicação dos fatores de capitalização (FAC), mesmo que calculados a juros simples, promove a capitalização composta (juros sobre juros). A distorção deste método fica mais visível quando fazemos a apuração dos Valores Atuais das prestações e comparamos o somatório destes valores (que representa o valor do investimento) com o valor emprestado. Podemos fazer isto de duas formas: (a) dividindo o valor das prestações pelo FAC de cada uma ou (b) multiplicando o valor de cada prestação pelo FVA de cada uma delas. Vamos, para efeito didático, escolher a segunda opção, cujos FVA já são conhecidos.
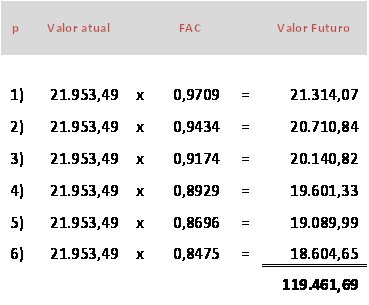
O valor total apurado é menor que o valor da operação, ou seja, a prestação de R$ 21.953,49 é adequada para uma operação de empréstimo de R$ 119.461,69.
Existe outra forma de observarmos que a prestação não serve como alternativa. Basta fazermos a decomposição do financiamento tomando como referencia o valor da prestação.
Vejamos:
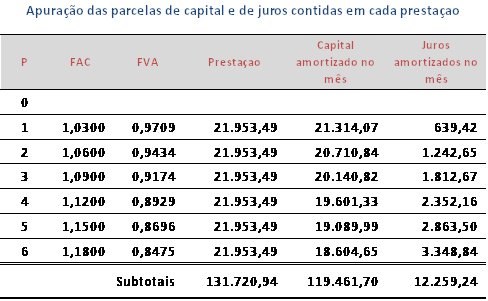
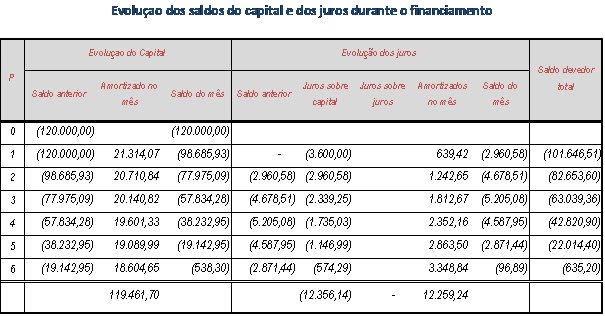
O quadro mostra que de fato a prestação é insuficiente para liquidar o empréstimo no prazo contratado. Veja que ao final do período ainda restaria um saldo devedor residual de R$ 635,20.
Conclusão
Talvez pelo fato de equalizar as prestações ao longo do financiamento, ou por engendrar um mecanismo complexo que torna difícil sua compreensão, fazendo com que a capitalização se dê de forma quase imperceptível, é que referidos colegas ainda compartilhem deste entendimento. O fato é que o SFA implica em efetiva capitalização composta de juros.
No método que descobri não ocorre a capitalização composta dos juros. Os saldos mensais não quitados pela prestação não são incorporados à base de cálculo dos juros do mês subsequente. Durante todo o financiamento os juros são mensalmente apropriados somente sobre os saldos mensais de capital.
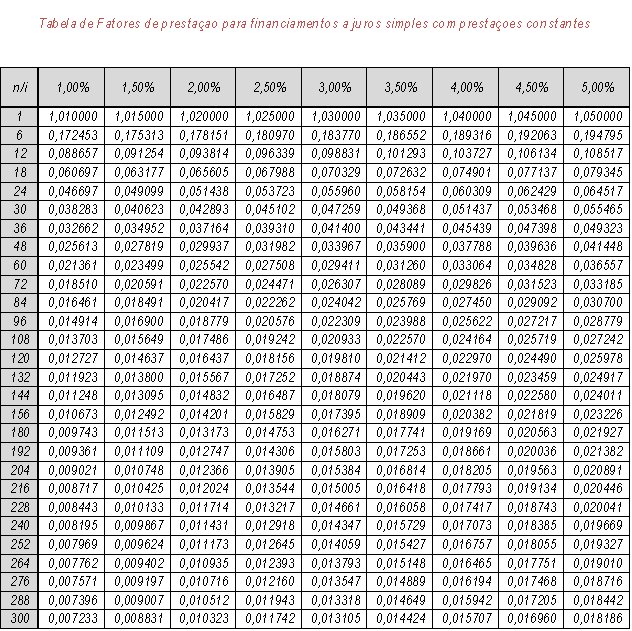
Por fim, ofereço uma tabela de fatores que poderá ser utilizada para se descobrir qual o valor ideal de prestação, para as taxas e períodos nela indicados.