A comprovação de que ocorre a capitalização composta dos juros na Tabela Price ainda tem gerado muita polemica. Há alguns anos escrevi alguns artigos nos quais tive como objetivo mostrar que no Sistema Francês de Amortização - que no Brasil ficou conhecido como Tabela Price - de fato ocorre a capitalização composta dos juros.
Vários trabalhos foram criados no sentido de indicar qual o método que poderia trazer a eficiência econômica e técnica da TP, sem, contudo, promover a capitalização composta dos juros.
Tenho visto, cada vez mais, colegas defendendo que um modelo matemático desenvolvido por Carl Friedrich Gauss alcança tal objetivo. Devo discordar: o método de Gauss é perfeito para outras aplicações matemáticas/estatísticas, mas não serve como alternativa à Tabela Price.
Em meus artigos, demonstro que existe uma forma simples de verificar se o modelo escolhido traz ou não em seu bojo a cobrança de juros compostos: estudo dos Fluxos de Caixa de uma Série de Pagamentos.
Assim, para facilitar o entendimento, proponho daqui para frente seguirmos estudando alguns exemplos e, a partir deles, evoluirmos em nossa compreensão. Primeiro faremos algumas simulações com juros compostos; depois partiremos para juros simples para, ao final, falarmos do Método de Gauss.

Valor Futuro = Valor Presente × (1 + i)^n
1. Juros compostos
1.1. Operações com uma única parcela
Exemplo 1
Empréstimo de R$ 120.000,00 a ser amortizado em uma única prestação ao final de 6 meses, com juros compostos de 3% ao mês, capitalizados mensalmente.

Aplicando a fórmula...
Valor Futuro = 120.000,00 × (1,03)^6 = 143.286,28
Assim, o devedor deverá pagar como única prestação ao final de 6 meses o valor de R$ 143.286,28 Agora, e se tivéssemos a situação contrária, ou seja, se quiséssemos saber o valor emprestado tendo as demais variáveis? Vejamos a seguir.
Exemplo 2
Empréstimo que será pago em uma única parcela de R$ 143.286,28 ao final de 6 meses, com juros compostos de 3% ao mês. Qual o valor emprestado?

Ajustando a fórmula temos a seguinte situação:
Valor Presente = Valor Futuro ÷ (1 + i)^n
Valor Presente = 143.286,28 ÷ (1,03)^6 = 120.000,00
Aplicando a fórmula no sentido contrário (apuração do Valor Presente a partir do Valor Futuro) se obteve o valor original da operação, confirmando, inclusive que ocorreu a capitalização composta dos juros.
1.2. Operações com várias parcelas
Exemplo 3
Compra de um imóvel no valor de R$ 120.000,00 a ser pago em 6 prestações com de R$ 20.000,00 cada uma que serão acrescidas de juros compostos de 3% ao mês. Qual será o valor das prestações em seus respectivos vencimentos?
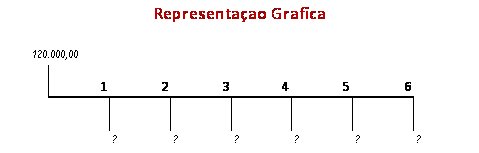
Numa Série de Pagamentos cada prestação pode ser analisada como se fosse uma operação independente. Neste como se tivéssemos vários empréstimos de mesmo valor sendo concedidos a uma mesma pessoa no mesmo dia, com prazos de vencimento diferenciados. Basta aplicarmos a taxa de 3% ao mês sobre cada uma das prestações de acordo com seus respectivos vencimentos e alcançaremos os valores devidos.
Ajustando a fórmula ao nosso exemplo, temos:
Valor Futuro m = Valor Presente m × (1 + i)^m
onde “m” representa o numero do termo
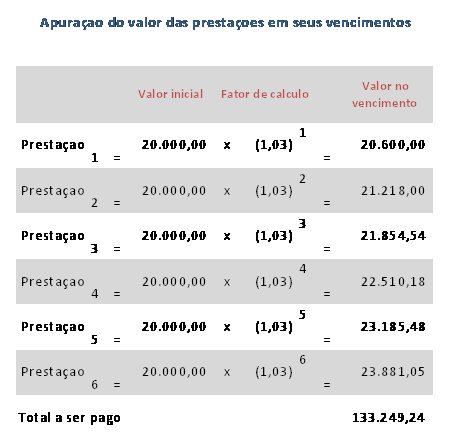
Vejamos agora a situação contrária: vamos apurar o Valor Presente da operação a partir das prestações e, ao mesmo tempo, confirmar se na operação ocorreu a capitalização composta dos juros
Exemplo 4
Compra de um imóvel cujo valor será pago em 6 prestações com valores crescentes conforme fluxo abaixo com juros compostos de 3% ao mês . Qual o valor financiado?

Neste caso o Valor Presente de cada prestação representa a parte do capital financiada por ela, e o somatório representa o total financiado. Para adequar a fórmula ao nosso exemplo precisamos fazer os seguintes ajustes.
Valor Presente m = Valor Futuro m ÷ (1 + i)^m
ou
VPm= VFm ÷ (1 + i)^m
Aplicando o raciocínio ao exemplo proposto, temos a seguinte situação
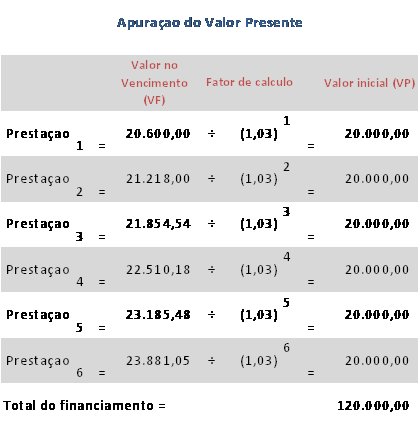
Exemplo 5
Compra de um imóvel cujo valor será pago em 6 prestações de valores decrescentes conforme fluxo abaixo, com juros compostos de 3% ao mês. Qual o valor financiado?

Aplicando o raciocínio temos...
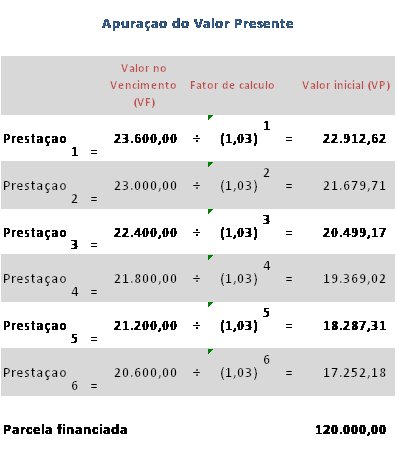
Exemplo 6
A compra de um determinado imóvel foi realizada mediante o pagamento de uma entrada mais 6 prestações mensais de R$ 22.151,70. Sabendo-se que foram cobrados juros compostos de 3% ao mês pergunta-se, qual a parcela financiada?

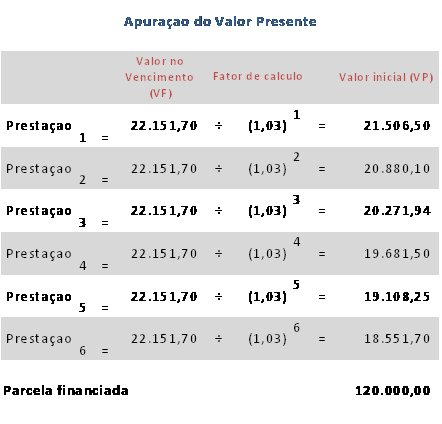
2. Juros simples
Até agora vimos aplicações com juros compostos. Vamos desenvolver o mesmo raciocínio em exemplos com juros simples:

Valor Futuro = Valor Presente × (1 + i × n)
2.1. Operações com única parcela
Exemplo 7
Empréstimo de R$ 120.000,00 a ser amortizado em uma única prestação ao final de 6 meses, com juros simples de 3% ao mês. Qual o valor total a ser pago?
.VF = 120.000,00 x (1 x 0,03 x 6) = 141.600,00
Total a ser pago = R$ 141.600,00
Exemplo 8
Empréstimo que será pago em uma única parcela de R$ 141.600,00 ao final de 6 meses, com juros compostos de 3% ao mês . Qual o valor emprestado?
Ajustando a fórmula temos...
Valor Presente = Valor Futuro ÷ (1+ i × n)
VP = 141.600,00 ÷ (1+ 0,03 × 6)
Valor financiado = R$ 120.000,00
2.2. Operações com várias parcelas
Exemplo 9
Compra de um imóvel no valor de R$ 120.000,00 a ser pago em 6 prestações de R$ 20.000,00 que serão acrescidas cada uma de juros simples de 3% ao mês. Qual será o valor das prestações em seus respectivos vencimentos e o valor total a ser pago?
Valor Futuro m = Valor Presente m × (1 + i × m)
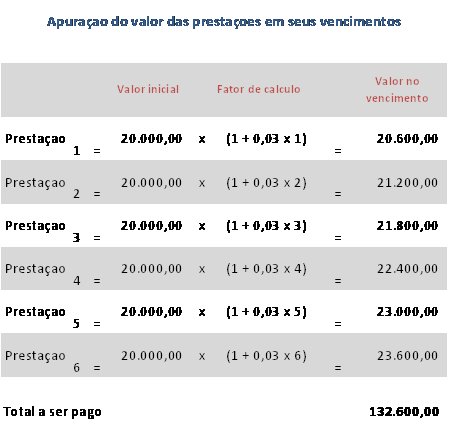
Exemplo 10
Compra de um imóvel cujo valor será pago em 6 parcelas conforme série abaixo com juros simples de 3% ao mês. Qual o valor financiado?

Ajustando e aplicando a fórmula dos juros simples no exemplo, alcançamos o seguinte resultado.
Valor Presente m = Valor Futuro m ÷ (1+ i × m)
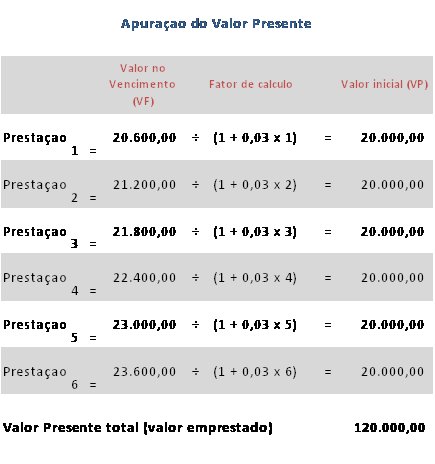
Exemplo 11
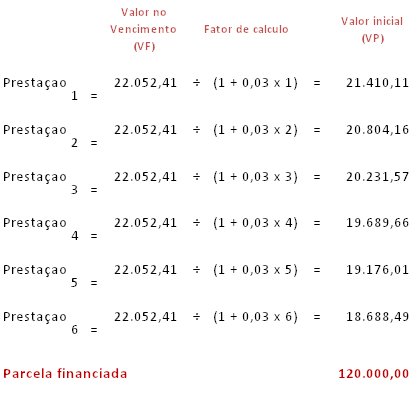
A compra de um determinado imóvel foi realizada mediante o pagamento de 6 prestações mensais de R$ 22.052,41 . Sabendo-se que foram cobrados juros simples de 3% ao mês pergunta-se, qual a parcela financiada?

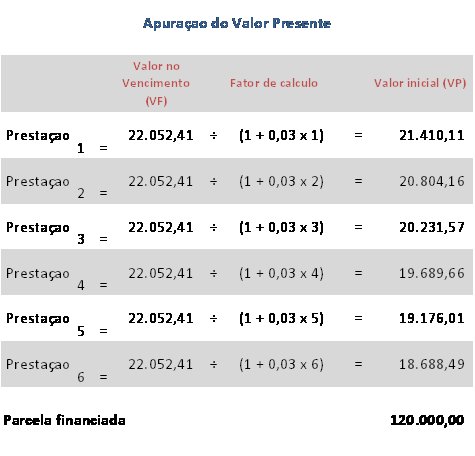
3. Método de Gauss
Todos os exemplos de séries de pagamentos sugeridos tomaram como referencia o valor financiado de R$ 120.000,00 com parcelamento em 6 prestações e juros de 3% ao mês. Por eles foi possível verificar as variações que surgem à medida que se muda formas de capitalização dos juros. Os exemplos 3 e 4 representam um financiamento realizado pelo SAC – Sistema de Amortização Constante com prestações crescentes. Os exemplos 5 e 6 representam parcelamentos feitos pelo SAC com prestações decrescentes e Tabela Price.
Vamos aplicar a fórmula do Método de Gauss no modelo proposto e examinar seus efeitos.

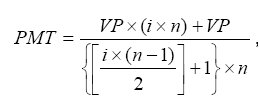
Aplicando a fórmula de Gauss...
Exemplo 12
A compra de um determinado imóvel de R$ 120.000,00 será realizada mediante o pagamento de 6 prestações mensais e iguais com juros de 3% ao mês, calculadas pelo Método de Gauss. Qual o valor das prestações?
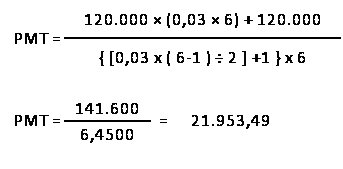
Testando a fórmula de Gauss pelo Método de Fluxos de Caixa ...
Exemplo 13
A compra de um determinado imóvel será realizada mediante o pagamento de 6 prestações mensais e iguais de R$ 21.953,49, Sabendo-se que foram cobrados juros simples de 3% ao mês pergunta-se, qual o valor financiado?

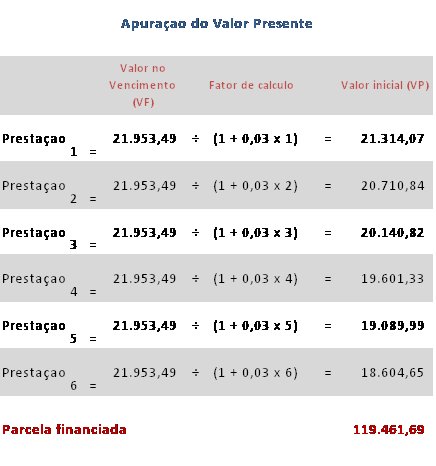
Examinando a série de pagamentos gerada pela aplicação do Método de Gauss observamos que o pagamento de 6 prestações mensais e iguais de R$ 21.953,49, a juros simples de 3% ao mês, não é suficiente para a liquidação do empréstimo. (O valor original é de R$ 120.000,00 e o valor apurado para a série de pagamentos foi de R$ 119.461,69). A prestação ideal teria que ser um pouco maior.
As prestações calculadas pelo Método de Gauss são sempre inferiores às necessárias para liquidar um empréstimo que evolui a juros simples
Então onde está o equivoco, já que o modelo matemático de Gauss também se baseia na Progressão Linear.
Para todo o tipo de operação de empréstimo existem dois agentes: quem tem os recursos e avalia as vantagens de conceder o empréstimo nas condições propostas, e quem demanda dos recursos e também avalia as condições.
Tendo em mente um determinado retorno financeiro o detentor dos recursos só decide a favor do parcelamento se alcançar o mesmo retorno financeiro que obteria pelo recebimento em uma única parcela.
Vejamos as operações descritas nos exemplos 1 e 6: o primeiro representa o pagamento de R$ 120.000,00 em única prestação após 6 meses; o segundo se refere ao pagamento do mesmo valor em 6 prestações mensais. Ambos com juros compostos de 3% ao mês.
Neste caso o detentor avaliará se o retorno em prestações será economicamente equivalente ao pagamento em uma prestação. E as contas que faz para decidir podem ser assim descritas.
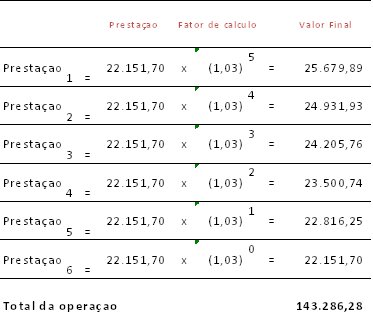
Para fazer este cálculo sobre cada uma das prestações deverão ser creditados juros desde o momento em ela foi paga até o final do período contratado. Considerando que os pagamentos começam 30 dias após a operação (final de cada período), sobre a primeira prestação serão creditados juros equivalente a 5 períodos; sobre a segunda serão creditados juros equivalentes a 4 períodos, e assim por diante.
Fazendo o cálculo como se o empréstimo fosse pago em uma única prestação havíamos alcançado o seguinte resultado:
Valor Futuro = 120.000,00 × (1,03)^6 = 143.286,28
Neste caso então o detentor dos recursos pode decidir a favor da concessão.
Vamos aplicar este mesmo raciocínio para o Método de Gauss. Fazendo o cálculo com juros simples e pagamento em uma única prestação, alcançamos o seguinte resultado (exemplo 7)
VF = 120.000,00 (1 x 0,03 x 6) = 141.600,00
O Método de Gauss se baseia na Soma de Termos de uma Progressão Aritmética. Partindo de um determinado valor (neste caso, R$ 141.600,00) ele permite calcular o valor do termo (prestação) cuja soma de uma determinada progressão aritmética aplicada sobre ele, resulte no valor esperado.
Calculando o retorno com base nas prestações calculadas pelo Método de Gauss, temos:
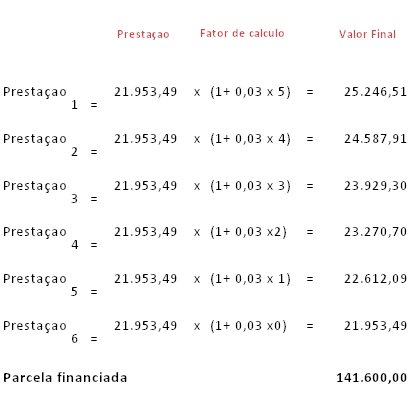
O cálculo do retorno do investimento é feito com base no valor cheio das parcelas. No Método de Gauss o termo que se apura com base da progressão aritmética será a prestação cheia. O problema está no fato de que em cada prestação existe uma parcela de juros que, pelo fato do cálculo da progressão aritmética ser feito sobre o valor cheio, estará sofrendo a incidência novos juros (juros sobre juros). Por isso, a prestação calculada pelo Método de Gauss é menor do que se o cálculo do retorno pudesse ser feito sem que os juros contidos em cada prestação sofressem a incidência de novos juros.
Assim, a prestação ideal para amortizar um empréstimo, a juros simples, será aquela que elimine os efeitos da capitalização composta tanto para quem busca os recursos financeiros (cálculo das prestações), quanto para quem está disposto a conceder o empréstimo (cálculo do retorno).
O problema proposto no exemplo 13 teve como objetivo verificar se a prestação calculada pelo Método de Gauss realmente servia para liquidar o empréstimo no tempo contratado. Aplicando as técnicas de Fluxos de Caixas verificamos que a prestação era menor no que a necessária. Pelas condições propostas, ela serviria para liquidar um empréstimo de R$ 119.461,69 (e não do valor original, R$ 120.000,00).
Vamos desenvolver um modelo de cálculo que elimine os efeitos da capitalização composta no cálculo do retorno do investimento para uma série proposta pelo Método de Gauss. Para facilitar a compreensão, dividiremos os cálculos em duas etapas, conforme seguem.
1ª etapa – Apurando os valores das parcelas do capital e dos juros embutidos em cada prestação
Para tanto, basta subtrairmos o VP apurado de cada prestação do valor cheio de cada prestação.
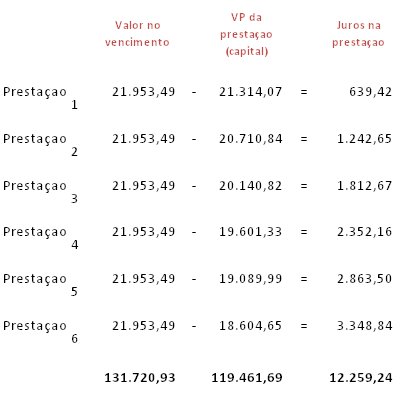
2ª etapa – Inibindo a apropriação de juros sobre os juros embutidos nas parcelas
Para tanto precisamos calcular os juros somente sobre a parcela de capital de cada prestação e, por fim, somar os juros embutidos nas prestações.
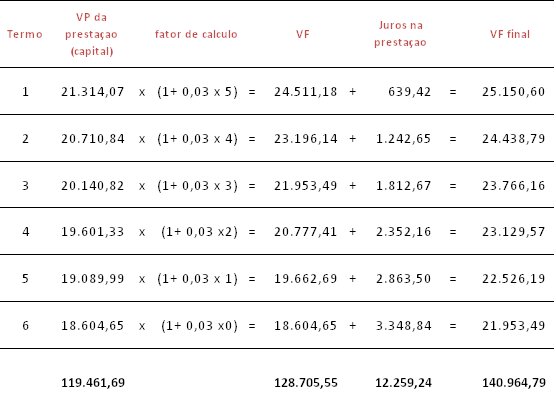
Fazendo o cálculo de maneira que os juros embutidos na prestação não sofressem novos juros (juros sobre juros) chegamos à conclusão final que, na verdade, o retorno do investimento por prestações calculadas pelo Método de Gauss é menor do que o retorno que se obteria com a amortização em uma única parcela.
Para que haja a plena aplicação dos conceitos de juros simples é necessário que não ocorra, nem no cálculo das prestações nem no cálculo do retorno do investimento, a apropriação de juros sobre juros. E, neste caso, devido aos preceitos sobre os quais ele foi montado, o Método de Gauss não serve como alternativa de juros simples.
Existe uma forma de calcular uma prestação que atenda a esta condição. No exemplo 11 temos esta situação. Para mostrar isto de forma mais clara vamos aplicar o raciocínio desenvolvido acima
No problema proposto temos a seguinte situação: financiamento de R$ 120.000,00 a juros simples de 3% ao mês, a ser pago em 6 prestações de R$ 22.052,41.
1º) Vamos apurar o valor do retorno do investimento se o empréstimo fosse pago em uma única parcela ao final de 6 meses
Valor Futuro = Valor Presente x (1 + i x n)
VF = 120.000,00 x (1 x 0,03 x 6) = 141.600,00
-
2º) Vamos apurar o VP de cada prestação (parcela de capital da prestação) e VP total (total emprestado), pelo Método de Fluxo de Caixa (para confirmar se a prestação irá amortizar/liquidar a operação no tempo certo)
Pelo cálculo acima foi possível comprovar que R$ 22.052,41 é o valor adequado para amortizar o empréstimo de R$ 120.000,00, nas condições sugeridas (juros simples de 3% ao mês em 6 prestações).
3º) Vamos calcular o retorno do investimento com base nas prestações, sem apropriar juros sobre os juros já embutidos nas prestações.
Para tanto, basta calcular os juros referentes à progressão aritmética somente sobre a parcela de capital de cada prestação e, ao final, somar os juros que já estavam embutidos em cada uma delas. Assim não estaremos apropriando juros sobre juros.
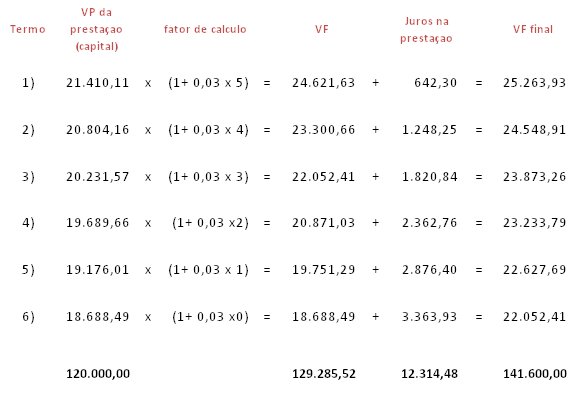
Verificamos que R$ 22.052,41 é o valor adequado para liquidar a operação, sem que haja a incidência de juros sobre juros tanto quando se calcula a prestação quanto se apura o retorno.
Conclusão
O Método de Gauss é um modelo de cálculo perfeito nas aplicações para as quais ele foi criado, mas não serve como alternativa de juros simples em operações financeiras.
Se levarmos em consideração que nas operações de empréstimo não pode haver a capitalização composta de juros, devemos supor que isto não pode ocorrer a favor de quem está fornecendo os recursos e nem a favor de quem os está recebendo.
O Método de Gauss toma como referência o retorno do investimento que um determinado valor poderá propiciar. Ocorre que, no caso de operações de empréstimos, as prestações são compostas de capital e juros, juros estes que, em razão dos cálculos que são feitos para apurar o retorno do investimento, sofrem a incidência de novos juros. Isto causa uma distorção a favor do devedor, na medida em que, justamente por causa da capitalização composta que ocorre no cálculo do retorno, para se alcançar o retorno esperado, a prestação calculada pelo Método de Gauss é menor.
Existe um modelo matemático através do qual podemos calcular uma prestação de igual valor pela qual seja possível amortizar um empréstimo a juros simples, tema que tratarei em outro artigo (A capitalização de juros nos sistemas de amortização adotados no Brasil).
Coloco-me à disposição de todos para esclarecimentos e discussões a respeito deste tema.